题目内容
17.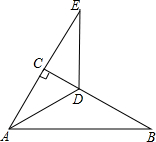 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.(1)求∠CAD的度数;
(2)延长AC至E,使AE=AB,求证:DA=DE.
分析 (1)根据题意可知∠CAB=60°,然后利用角平分线性质可求得答案;
(2)由题意可知三角形ABE是等边三角形,然后在证明Rt△DCA≌Rt△DCE,即可求证.
解答  解:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,
解:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,
∴∠CAB=60°=2×∠CAD,
∴∠CAD=30°;
(2)连接BE,得到三角形ABE,
∵延长AC至E,使AE=AB,在Rt△ABC中,∠ACB=90°,∠B=30°,
∴∠EAB=60°,
∴三角形ABE是等边三角形,
∴AC=CE,
∴Rt△DCA≌Rt△DCE,
∴DA=DE.
点评 本题主要考查了含30°角的直角三角形,解题的关键是掌握角平分线的性质以及等边三角形的性质,此题难度不大.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
8. 如图,已知点P到BE、BD、AC的距离恰好相等,则点P的位置:
如图,已知点P到BE、BD、AC的距离恰好相等,则点P的位置:
①在∠B的平分线上;
②在∠DAC的平分线上;
③在∠EAC的平分线上;
④恰是∠B,∠DAC,∠EAC三个角的平分线的交点.
上述结论中,正确结论的个数有( )
 如图,已知点P到BE、BD、AC的距离恰好相等,则点P的位置:
如图,已知点P到BE、BD、AC的距离恰好相等,则点P的位置:①在∠B的平分线上;
②在∠DAC的平分线上;
③在∠EAC的平分线上;
④恰是∠B,∠DAC,∠EAC三个角的平分线的交点.
上述结论中,正确结论的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5. 如图,在平面直角坐标系中,点A(4,3),点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )
如图,在平面直角坐标系中,点A(4,3),点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )
 如图,在平面直角坐标系中,点A(4,3),点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )
如图,在平面直角坐标系中,点A(4,3),点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
2.在△ABC中,∠C=90°,以点B为圆心,以BC长为半径作圆,点A与该圆的位置关系为( )
| A. | 点A在圆外 | B. | 点A在圆内 | C. | 点A在圆上 | D. | 无法确定 |
9. 有理数a,b在数轴上的位置如图所示,则下列结论中,正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论中,正确的是( )
 有理数a,b在数轴上的位置如图所示,则下列结论中,正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论中,正确的是( )| A. | a-b>0 | B. | a+b>0 | C. | $\frac{a}{b}$>0 | D. | |a|>|b| |
6.(-1,y1),(2,y2)与(3,y3)为二次函数y=-x2-4x+5图象上的三点,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
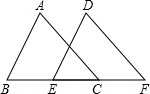 如图BC=EF,AC=DF,要证明△ABC≌△DEF,还需添加一个条件:
如图BC=EF,AC=DF,要证明△ABC≌△DEF,还需添加一个条件: 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2)与B点.若C是y轴上的点,且满足△ABC的面积为10,则C点坐标为(0,1)或(0,-9).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2)与B点.若C是y轴上的点,且满足△ABC的面积为10,则C点坐标为(0,1)或(0,-9).