题目内容
12. 如图,如图在△ABC中,△PDE的周长为5,BP,CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则BC的长为5.
如图,如图在△ABC中,△PDE的周长为5,BP,CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则BC的长为5.
分析 可利用角平分线的性质与平行线的性质得出∠PBD=∠BPD,∠PCE=∠EPC,进而得出PD=BD,PE=CE,故可求解.
解答 解:∵BP、CP分别平分∠ABC、∠ACB,
∴∠ABP=∠PBD,∠ACP=∠PCE,
又PD∥AB,PE∥AC,
∴∠ABP=∠BPD,∠APC=∠EPC,
∴∠PBD=∠BPD,∠PCE=∠EPC,
∴PD=BD,PE=CE,
∴BC=BD+DE+EC=PD+DE+PE=△PDE的周长=5,
故答案为:5.
点评 此题主要考查等腰三角形的性质,涉及的知识点有:角平分线及平行线的性质.能够发现△BDP和△PEC是等腰三角形是解答此题的关键.

练习册系列答案
相关题目
3.下列各式从左到右的变形中,是因式分解的是( )
| A. | (a+3)(a-3)=a2-9 | B. | m2-m+2=m(m-1+$\frac{2}{m}$) | C. | a2-4a-5=a(a-4)-5 | D. | a2-4a+4=(a-2)2 |
17.一位鞋店的经理,为了解鞋子的销售情况,随机调查了一个月销售的鞋子的尺码,对这组数据的分析中,鞋店的经理最感兴趣的是这组数据的( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
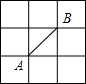 如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果点C也是图中的格点,且使得△ABC为等腰直角三角形,则点C的个数是( )
如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果点C也是图中的格点,且使得△ABC为等腰直角三角形,则点C的个数是( )