题目内容
17．在Rt△ABC中，已知∠C=90°，a=16，c=28，解这个直角三角形．分析 首先根据勾股定理推出b的长度，然后根据a和c的关系即可推出∠A的度数，既而求出∠B的度数．
解答 
解：∵∠C=90°，a=16，c=28，
由勾股定理得：b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{2{8}^{2}-1{6}^{2}}$=4$\sqrt{33}$，
∴sinA=$\frac{a}{c}$=$\frac{16}{28}$≈0.5943，
∴∠A≈37°，
∴∠B=90°-∠A=53°．
点评 本题考查了解直角三角形，勾股定理的应用，能通过解直角三角形求出sinA是解此题的关键，难度适中．
练习册系列答案
相关题目
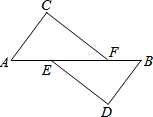已知，如图：A、E、F、B在一条直线上，AE=BF，∠C=∠B，CF∥DE，
如图，如图在△ABC中，△PDE的周长为5，BP，CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则BC的长为5．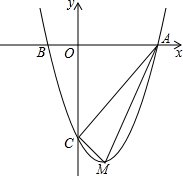
如图，已知二次函数的图象与x轴的交点横坐标为方程x2-4x-12=0的两根，与y轴交于点C（0，-8）．
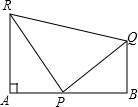如图，RA⊥AB，QB⊥AB，P是AB上的一点，RP=PQ=a，RA=h，QB=k，∠RPA=75°，∠QPB=45°，求AB的长度．