题目内容
4.已知$\frac{{x}^{2}+1}{x}$=$\sqrt{5}$,求$\frac{{x}^{4}+{x}^{2}+1}{{x}^{4}-{x}^{2}+1}$的值.分析 先根据$\frac{{x}^{2}+1}{x}$=$\sqrt{5}$得出x+$\frac{1}{x}$=$\sqrt{5}$,再把代数式的分子分母同时除以x2,把x+$\frac{1}{x}$=$\sqrt{5}$代入进行计算即可.
解答 解:∵$\frac{{x}^{2}+1}{x}$=$\sqrt{5}$,
∴x+$\frac{1}{x}$=$\sqrt{5}$,
∴原式=$\frac{{x}^{2}+\frac{1}{{x}^{2}}+1}{{x}^{2}+\frac{1}{{x}^{2}}-1}$
=$\frac{(x+\frac{1}{x})^{2}-2+1}{(x+\frac{1}{x})^{2}-2-1}$
=$\frac{(\sqrt{5})^{2}-2+1}{(\sqrt{5})^{2}-2-1}$
=$\frac{5-2+1}{5-2-1}$
=$\frac{4}{2}$
=4.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
15.下列计算中正确的是( )
| A. | a2•a3=a6 | B. | (-ab)2=-a2b2 | C. | a2+a3=a5 | D. | a3÷a2=a |
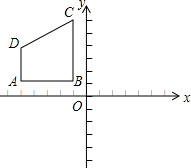 如图,四边形ABCD的顶点坐标为A(-5,1),B(-1,1),C(-1,6),D(-5,4),请作出四边形ABCD关于x轴的对称图形四边形A1B1C1D1,并写出A1B1C1D1点的坐标.
如图,四边形ABCD的顶点坐标为A(-5,1),B(-1,1),C(-1,6),D(-5,4),请作出四边形ABCD关于x轴的对称图形四边形A1B1C1D1,并写出A1B1C1D1点的坐标. 如图,如图在△ABC中,△PDE的周长为5,BP,CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则BC的长为5.
如图,如图在△ABC中,△PDE的周长为5,BP,CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则BC的长为5.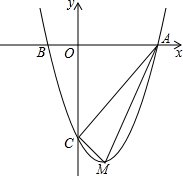 如图,已知二次函数的图象与x轴的交点横坐标为方程x2-4x-12=0的两根,与y轴交于点C(0,-8).
如图,已知二次函数的图象与x轴的交点横坐标为方程x2-4x-12=0的两根,与y轴交于点C(0,-8).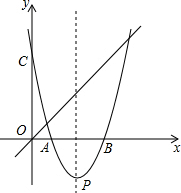 已知二次函数的图象经过A(2,0)、C(0,12)两点,且对称轴为直线x=4.设顶点为点P,与x轴的另一交点为点B.
已知二次函数的图象经过A(2,0)、C(0,12)两点,且对称轴为直线x=4.设顶点为点P,与x轴的另一交点为点B.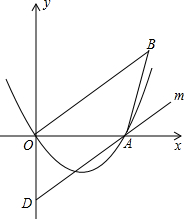 如图,已知等腰△AOB中,AB=AO=4,tan∠AOB=$\frac{3}{4}$,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
如图,已知等腰△AOB中,AB=AO=4,tan∠AOB=$\frac{3}{4}$,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).