题目内容
8.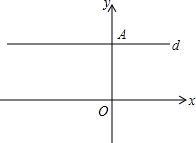 如图,在平面直角坐标系中,点O为坐标原点,A(0,a),B(b,0),a与b为方程组$\left\{\begin{array}{l}{4a+3b=-11}\\{a+b=-5}\end{array}\right.$的解,过点A作x轴的平行线d
如图,在平面直角坐标系中,点O为坐标原点,A(0,a),B(b,0),a与b为方程组$\left\{\begin{array}{l}{4a+3b=-11}\\{a+b=-5}\end{array}\right.$的解,过点A作x轴的平行线d(1)求点A、B的坐标;
(2)动点P从B出发沿x轴正方形运动,速度为2个单位/秒,设运动时间为t秒,△POA的面积为S,求出用t表示S的关系式(并直接写出相应的t的取值范围);
(3)在(2)的条件下,若动点Q同时从A出发沿射线AO方向运动,速度为4个单位/秒,在直线d上有动点R,问t为何值时,以P、Q、R为顶点的三角形是等腰直角三角形(PQ为底),并求出此时点P的坐标.
分析 (1)求出方程组中中a、b的值即可得出A、B两点的坐标;
(2)分0≤t<$\frac{9}{2}$与t≥$\frac{9}{2}$两种情况进行讨论;
(3)设R(-x,4),当0≤t≤4.5时,设P(9-2t,0),Q(0,4-4t),D(9-2t,4),则AQ=4t,PD=4,AR=-x,DR=9-2t+x,当△PRQ时以PQ为底的等腰直角三角形时可得出△ARQ≌△DPR,求出t的值;当t>4.5时,不存在以PQ为底的等腰直角三角形PRQ.
解答 解:(1)解方程组$\left\{\begin{array}{l}{4a+3b=-11}\\{a+b=-5}\end{array}\right.$得:$\left\{\begin{array}{l}{a=4}\\{b=-9}\end{array}\right.$,
则A的坐标是(0,4),B的坐标是(-9,0);
(2)当0≤t<$\frac{9}{2}$时,P在线段OB上,OP=9-2t,则S=$\frac{1}{2}$×4(9-2t),即S=-4t+18;
当t≥$\frac{9}{2}$时,P在BO的延长线上,OP=2t-9,则S=$\frac{1}{2}$×4(2t-9),即S=4t-18;
综上所述,S=$\left\{\begin{array}{l}18-4t(0≤t<4.5)\\ 4t-18(t≥4.5)\end{array}\right.$;
(3)如图所示,设R(-x,4),
当0≤t≤4.5时,设P(9-2t,0),Q(0,4-4t),D(9-2t,4),则AQ=4t,PD=4,AR=-x,DR=9-2t+x,当△PRQ时以PQ为底的等腰直角三角形时,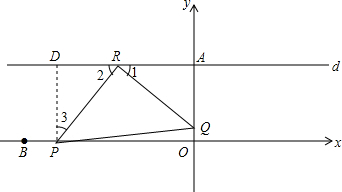
∵PR=QR,∠PRQ=90°,
∴∠1+∠2=∠2+∠3=90°,
∴∠1=∠3.
同理,∠2=∠AQR.
在△ARQ与△DPR中,
∵$\left\{\begin{array}{l}∠1=∠3\\ QR=PR\\∠AQR=∠2\end{array}\right.$,
∴△ARQ≌△DPR(ASA),
∴DP=AR,DR=AQ,即$\left\{\begin{array}{l}x=-4\\ 9-2t+x=4t\end{array}\right.$,解得t=$\frac{5}{6}$,
∴P(-$\frac{22}{3}$,0).
当t>4.5时,不存在以PQ为底的等腰直角三角形PRQ.
点评 本题考查的是一次函数综合题,涉及到一次函数图象上点的坐标特点及全等三角形的判定与性质等知识,在解答(2)(3)时要注意进行分类讨论.

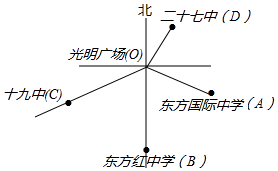 小明在光明广场(点O)绘制了市内几座学校相对广场的位置简图,(图中1cm表示5km),东方红中学在广场正南方向,测得OA=1.7cm,OB=2cm,OC=2cm,OD=1.4cm,∠AOC=123°18′,∠BOA=68°24′,∠AOD=88°28′,如何确定每个学校的具体位置?
小明在光明广场(点O)绘制了市内几座学校相对广场的位置简图,(图中1cm表示5km),东方红中学在广场正南方向,测得OA=1.7cm,OB=2cm,OC=2cm,OD=1.4cm,∠AOC=123°18′,∠BOA=68°24′,∠AOD=88°28′,如何确定每个学校的具体位置?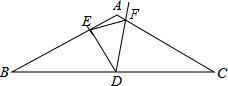 已知:△ABC中,AB=AC,∠BAC=120°,D为BC的中点,且∠EDF=∠C.
已知:△ABC中,AB=AC,∠BAC=120°,D为BC的中点,且∠EDF=∠C. 如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.
如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.