题目内容
19.一个不透明的袋子里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球2个(分别标有1号、2号)蓝球1个,黄球1个.从口袋中任意摸出一个球,记下颜色后放回,再从口袋中随机摸出一个.(1)请用画树状图或列表法,列出所有可能的情况;
(2)求两次摸到不同颜色球的概率.
分析 (1)列表将所有等可能的结果列举出来即可,注意是一个放回实验;
(2)根据列表,将所有颜色不同的情况找出来,利用概率公式直接求解即可.
解答 解:(1)列表如下:
| 红1 | 红2 | 黄 | 蓝 | |
| 红1 | (红1,红1) | (红1,红2) | (红1,黄) | (红1,蓝) |
| 红2 | (红2,红1) | (红2,红2) | (红2,黄) | (红2,蓝) |
| 黄 | (黄,红1) | (黄,红2) | (黄,黄) | (黄,蓝) |
| 蓝 | (蓝,红1) | (蓝,红2) | (蓝,黄) | (蓝,蓝) |
则P=$\frac{10}{16}$=$\frac{5}{8}$.
点评 此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.一元二次方程x2+2=0的根的情况为( )
| A. | 没有实根 | B. | 有两个相等的实根 | ||
| C. | 有两个不等的实根 | D. | 有两个实根 |
6.下列运算中,正确的是( )
| A. | b3•b3=b9 | B. | (-x3y)•(xy2)=x4y3 | C. | (-2x3)2=-4x6 | D. | (-a2)3=-a6 |
7.在△ABC中,已知∠A=60°,BD⊥AC于点D,CE⊥AB于点E,且BD=CE,则△ABC是( )
| A. | 不等边三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 直角三角形 |
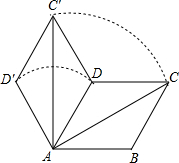 如图,菱形ABCD的边长为4,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连结DC′.
如图,菱形ABCD的边长为4,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连结DC′.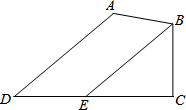 已知:如图,在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,BE∥AD交CD于点E.求证:BE平分∠ABC.
已知:如图,在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,BE∥AD交CD于点E.求证:BE平分∠ABC.
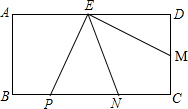 已知矩形ABCD中,AD=2AB,AB=6,E为AD中点,M为CD上一点,PE⊥EM交CB于点P,EN平分∠PEM交BC于点N.
已知矩形ABCD中,AD=2AB,AB=6,E为AD中点,M为CD上一点,PE⊥EM交CB于点P,EN平分∠PEM交BC于点N.