题目内容
15．解关于x的不等式：x2+（a2+a）x+a3＞0．分析 分-a≥-a2和-a＜-a2两种情况考虑，当-a≥-a2时，解不等式求出x的取值范围；当-a＜-a2时，解不等式求出x的取值范围．此题得解．
解答 解：x2+（a2+a）x+a3=（x+a2）（x+a）＞0，
当-a≥-a2，即a≤0或a≥1时，
x＜-a2或x＞-a；
当-a＜-a2，即0＜a＜1时，
x＜-a或x＞-a2．
点评 本题考查了一元二次不等式，分-a≥-a2和-a＜-a2两种情况考虑是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
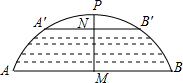如图所示，有一座拱桥圆弧形，它的跨度AB为60米，拱高PM为18米，当洪水泛滥到跨度只有30米时，就要采取紧急措施，若拱顶离水面只有4米，即PN=4米时，是否采取紧急措施？（$\sqrt{2}$=1.414）
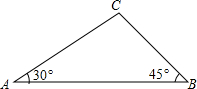如图，在△ABC中，∠A=30°，∠B=45°，AC=2$\sqrt{3}$，则CB的长为$\sqrt{6}$．
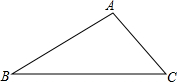如图，在△ABC中，已知∠B=30°，∠C=45°，AB=6，AC=3$\sqrt{2}$，求BC的长．
4．某公司2007年的利润是a万元，计划以后每年在前一年的基础上增长m%，则2010年的利润是（ ）
| A． | a（1+m%）2 | B． | a（1+m%）3 | C． | a（1+m%）4 | D． | （a+m%）3 |
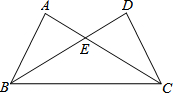如图，在△ABC与△DCB中，AC与BD交于点E，且∠A=∠D=90°，AB=DC．