题目内容
19.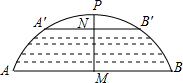 如图所示,有一座拱桥圆弧形,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,是否采取紧急措施?($\sqrt{2}$=1.414)
如图所示,有一座拱桥圆弧形,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,是否采取紧急措施?($\sqrt{2}$=1.414)
分析 由垂径定理可知AM=BM、A′N=B′N,利用AB=60,PM=18,可先求得圆弧所在圆的半径,再计算当PN=4时A′B′的长度,与30米进行比较大小即可.
解答 解:
设圆弧所在圆的圆心为O,连接OA、OA′,设半径为x米,
则OA=OA′=OP′,
由垂径定理可知AM=BM,A′N=B′N,
∵AB=60米,
∴AM=30米,且OM=OP-PM=(x-18)米,
在Rt△AOM中,由勾股定理可得AO2=OM2+AM2,
即x2=(x-18)2+302,解得x=34,
∴ON=OP-PN=34-4=30(米),
在Rt△A′ON中,由勾股定理可得A′N=$\sqrt{O{A}^{′2}-O{N}^{2}}$=$\sqrt{3{4}^{2}-3{0}^{2}}$=16(米),
∴A′B′=32米>30米,
∴不需要采取紧急措施.
点评 本题主要考查垂径定理的应用,利用勾股定理求得圆弧所在的半径是解题的关键,注意方程思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
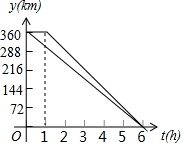 在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲、乙两车分别从A、B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.当甲车出发3.5小时时,两车相距330km.
在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲、乙两车分别从A、B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.当甲车出发3.5小时时,两车相距330km. 如图,一次函数y=x与二次函数y=ax2+bx+c图象相交于A、B两点,则函数y=ax2+(b-1)x+c的图象可能是( )
如图,一次函数y=x与二次函数y=ax2+bx+c图象相交于A、B两点,则函数y=ax2+(b-1)x+c的图象可能是( )