题目内容
19.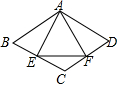 如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,下列结论:①AE=AF;②∠EAF=60°;③△CEF是等腰三角形;④AF=$\sqrt{3}$cm,其中结论正确的个数是( )
如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,下列结论:①AE=AF;②∠EAF=60°;③△CEF是等腰三角形;④AF=$\sqrt{3}$cm,其中结论正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 连接AC,则△ABC和△ACD是两个全等是等边三角形,以及三线合一定理,利用三角函数即可求解、判断.
解答  解:连接AC.
解:连接AC.
∵菱形ABCD中,AB=BC,∠B=60°,
∴△ABC和△ACD都是等边三角形.
即AB=BC=CD=AD=AC.
又∵E、F是BC和CD的中点,
∴CE=CF,
∴△CEF是等腰三角形,故③正确.
∵等边△ABC中,E是BC的中点,
∴∠EAC=$\frac{1}{2}$∠BAC=30°,AE=AB•sin∠B=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$(cm).
同理∠FAC=30°,AF=$\sqrt{3}$.故④正确;
则∠EAF=60°,AE=AF故①②正确;
故选D.
点评 本题考查了菱形的性质,理解△ABC和△ACD是两个全等是等边三角形是关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
9.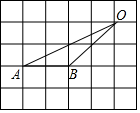 在下列网格中,小正方形的边长为1,点A,B,O都在格点上,求∠A的余弦值( )
在下列网格中,小正方形的边长为1,点A,B,O都在格点上,求∠A的余弦值( )
 在下列网格中,小正方形的边长为1,点A,B,O都在格点上,求∠A的余弦值( )
在下列网格中,小正方形的边长为1,点A,B,O都在格点上,求∠A的余弦值( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{10}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
 如图,点D在BC的延长线上,DF∥CA,∠EDF=∠A,请你判断DE与BA的位置关系,并证明你的结论.
如图,点D在BC的延长线上,DF∥CA,∠EDF=∠A,请你判断DE与BA的位置关系,并证明你的结论.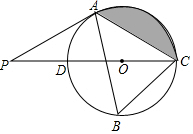 如图,在⊙O的内接三角形ABC中,∠ABC=60°,AC=5,过点A作⊙O的切线交直径CD的延长线于点P.
如图,在⊙O的内接三角形ABC中,∠ABC=60°,AC=5,过点A作⊙O的切线交直径CD的延长线于点P. (1)解方程:$\frac{1}{x-2}$+$\frac{x+2}{2-x}$=2
(1)解方程:$\frac{1}{x-2}$+$\frac{x+2}{2-x}$=2