题目内容
10.某单位计划从文具用品商店购买同一种类的钢笔和笔记本,已知购买一支钢笔比购买一个笔记本多用20元,若用400元购买钢笔和用160元购买笔记本,则购买钢笔的数量是购买笔记本数量的一半.(1)求购买一支钢笔、一个笔记本各需要多少元?
(2)经商谈,商店给予优惠,优惠方式是每购买一支钢笔赠送一个笔记本;如果此单位需要笔记本的数量是钢笔数量的2倍还多8个,且购买钢笔和笔记本的总费用不超过670元,那么最多可购买多少支钢笔?
分析 (1)设购一个笔记本为x元,则一支钢笔为(x+20)元,根据用400元购买钢笔和用160元购买笔记本,则购买钢笔的数量是购买笔记本数量的一半列出方程解答即可;
(2)设最多可购买a支钢笔,根据购买钢笔和笔记本的总费用不超过670元列出不等式解答即可.
解答 解:(1)设购一个笔记本为x元,则一支钢笔为(x+20)元.
由题意得:$\frac{400}{x+20}$=$\frac{160}{2x}$,
解得:x=5,
经检验,x=5是原方程得解.
∴购买一支钢笔为x+20=25(元)
答:购一个笔记本为5元,则一支钢笔为25元.
(2)设最多可购买a支钢笔.
由题意得:25a+5(2a+8-a)≤670
解得:a≤21.
答:最多可购买21支钢笔.
点评 此题考查分式方程的实际运用,一元一次不等式的实际运用,找出题目蕴含的等量关系和不等关系是解决问题的关键.

练习册系列答案
相关题目
20.计算|-6|-(-$\frac{1}{3}$)0的值是( )
| A. | 5 | B. | -5 | C. | 5$\frac{2}{3}$ | D. | 7 |
1. 如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
 如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
5.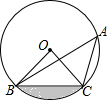 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )| A. | π-2 | B. | $\frac{2}{3}π-1$ | C. | π-4 | D. | $\frac{2}{3}π-2$ |
15.已知a+b+c=0,则$\frac{\sqrt{{a}^{2}}}{a}+\frac{\sqrt{{b}^{2}}}{b}+\frac{\sqrt{{c}^{2}}}{c}$的值可能是1或-1.
2. 在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A→B→C→D→A…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),当蚂蚁爬了2017个单位时,它所处位置的坐标为( )
在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A→B→C→D→A…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),当蚂蚁爬了2017个单位时,它所处位置的坐标为( )
 在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A→B→C→D→A…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),当蚂蚁爬了2017个单位时,它所处位置的坐标为( )
在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A→B→C→D→A…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),当蚂蚁爬了2017个单位时,它所处位置的坐标为( )| A. | (1,1) | B. | (1,0) | C. | (0,1) | D. | (0,-1) |
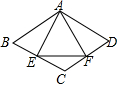 如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,下列结论:①AE=AF;②∠EAF=60°;③△CEF是等腰三角形;④AF=$\sqrt{3}$cm,其中结论正确的个数是( )
如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,下列结论:①AE=AF;②∠EAF=60°;③△CEF是等腰三角形;④AF=$\sqrt{3}$cm,其中结论正确的个数是( ) 在△ABC中,∠ABC,∠ACB的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=30°;∠E=60°.
在△ABC中,∠ABC,∠ACB的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=30°;∠E=60°.