题目内容
8.定义:a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数.如:2的差倒数是$\frac{1}{1-2}$=-1,-1的差倒数是$\frac{1}{1-(-1)}$=$\frac{1}{2}$.已知a1=-$\frac{1}{3}$,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推an+1是an的差倒数,请你直接写出a2016=4.分析 求出数列的前4项,继而得出数列的循环周期,然后求解可得.
解答 解:∵a1=-$\frac{1}{3}$,
a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1+\frac{1}{3}}$=$\frac{3}{4}$,
a3=$\frac{1}{1-{a}_{2}}$=$\frac{1}{1-\frac{3}{4}}$=4,
a4=$\frac{1}{1-{a}_{3}}$=$\frac{1}{1-4}$=-$\frac{1}{3}$,
…,
∴这列数每3个数为一周期循环,
∵2016÷3=672,
∴a2016=a3=4.
故答案为:4.
点评 本题主要考查数字的变化规律,解决此类问题时通常需要确定数列与序数的关系或者数列的循环周期等,此题得出这列数每3个数为一周期循环是解题的关键.

练习册系列答案
相关题目
16.李明靠勤工俭学的收入支付生活费,下面是李明一周的收支情况表(收入为正,支出为负,单位为元)
(1)在一周内李明有多少结余?
(2)照这样,一个月(按30天计算)李明能有多少结余?
| 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| +15 | +10 | 0 | +20 | +15 | +10 | +17 |
| -8 | -12 | -10 | -7 | -9 | -8 | -10 |
(2)照这样,一个月(按30天计算)李明能有多少结余?
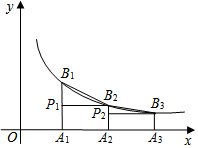 如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3═An-1An=1,分别过点A1、A2、A3、…、An作x轴的垂线,交反比例函数y=$\frac{2}{x}$(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2017=$\frac{2017}{2018}$.
如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3═An-1An=1,分别过点A1、A2、A3、…、An作x轴的垂线,交反比例函数y=$\frac{2}{x}$(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2017=$\frac{2017}{2018}$.
