题目内容
10. 请在方格内画出△ABC,使它的顶点都在格点上,且三边长1,$\sqrt{2}$,$\sqrt{5}$,
请在方格内画出△ABC,使它的顶点都在格点上,且三边长1,$\sqrt{2}$,$\sqrt{5}$,①求△ABC的面积; ②求出最长边上的高.
分析 ①所作△ABC如图所示,延长BA,过点C作CP⊥AP交BA延长线于点P,根据三角形的面积公式求解可得;
②作AH⊥BC,由S△ABC=$\frac{1}{2}$BC•AH=$\frac{1}{2}$且BC=$\sqrt{5}$可得AH的长.
解答 解:①如图所示,△ABC即为所求,其中AB=1、AC=$\sqrt{2}$、BC=$\sqrt{5}$,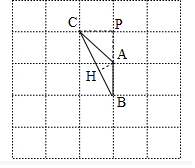
延长BA,过点C作CP⊥AP交BA延长线于点P,
S△ABC=$\frac{1}{2}$×AB×CP=$\frac{1}{2}$×1×1=$\frac{1}{2}$;
②如图,过点A作AH⊥BC于点H,
∵S△ABC=$\frac{1}{2}$BC•AH=$\frac{1}{2}$,且BC=$\sqrt{5}$,
∴AH=$\frac{\sqrt{5}}{5}$,
∴最长边上的高为$\frac{\sqrt{5}}{5}$.
点评 本题主要考查作图-应用与设计作图,熟练掌握勾股定理和三角形的面积公式是解题的关键.

练习册系列答案
相关题目
15.将分式方程$\frac{x}{x-2}$-$\frac{2}{2-x}$=3化为整式方程,正确的是( )
| A. | x-2=3 | B. | x+2=3 | C. | x-2=3(x-2) | D. | x+2=3(x-2) |
1.计算-$\frac{{6}^{2}}{7}$的值为( )
| A. | -$\frac{36}{7}$ | B. | $\frac{36}{7}$ | C. | $\frac{36}{49}$ | D. | -$\frac{36}{49}$ |
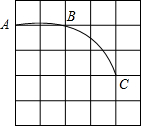 如图,在5×5的正方形网格中,每个小正方形的边长为1,一段圆弧经过格点A、B、C,请完成下列任务.
如图,在5×5的正方形网格中,每个小正方形的边长为1,一段圆弧经过格点A、B、C,请完成下列任务.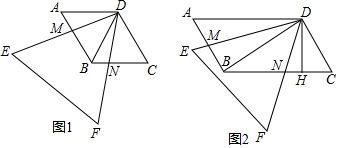
 如图,在△ABC中,∠A=40°,∠C=64°,DE是AB的中垂线,则∠DBC=32度.
如图,在△ABC中,∠A=40°,∠C=64°,DE是AB的中垂线,则∠DBC=32度. 如图,在五边形ABCDE中,AP平分∠EAB,BP平分∠ABC.
如图,在五边形ABCDE中,AP平分∠EAB,BP平分∠ABC.