题目内容
15. 如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.
如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.(1)若∠B=30°,∠C=50°,求∠DAE的度数.
(2)若∠C>∠B,猜想∠DAE与∠C-∠B之间的数量关系,并直接写出结论.
分析 (1)先根据三角形内角和得到∠CAB=180°-∠B-∠C=100°,再根据角平分线与高线的定义得到∠CAE=$\frac{1}{2}$∠CAB=50°,∠ADC=90°,则∠CAD=90°-∠C=40°,然后利用∠DAE=∠CAE-∠CAD计算即可.
(2)根据题意可以用∠B和∠C表示出∠CAD和∠CAE,从而可以得到∠DAE与∠C-∠B的关系.
解答  解:∵∠ABC=30°,∠ACB=50°,
解:∵∠ABC=30°,∠ACB=50°,
∴∠CAB=180°-∠B-∠C=100°,
∵AE是△ABC角平分线,
∴∠CAE=$\frac{1}{2}$∠CAB=50°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°-∠C=40°,
∴∠DAE=∠CAE-∠CAD=50°-40°=10°.
(2)∠DAE=$\frac{1}{2}$(∠ACB-∠ABC),
理由:∵在△ABC中,AD,AE分别是△ABC的高和角平分线,
∴∠CAB=180°-∠B-∠C,∠CAD=90°-∠C,∠CAE=$\frac{1}{2}$(180°-∠B-∠C),
∴∠DAE=$\frac{1}{2}$(180°-∠B-∠C)-(90°-∠C)=$\frac{1}{2}$(∠C-∠B).
点评 本题考查三角形内角和定理、角的平分线的性质、直角三角形的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
5.在比例尺是1:500的图纸上,测得一块长方形的土地长5厘米,宽4厘米,这块地的实际面积是( )平方米.
| A. | 20平方米 | B. | 500平方米 | C. | 5000平方米 | D. | 500000平方米 |
3.当-1≤x≤2时,二次函数y=x2+2mx+m+2,有最小值-3,则实数m的值为( )
| A. | $\frac{1+\sqrt{21}}{2}$或$\frac{1-\sqrt{21}}{2}$ | B. | 6或-$\frac{9}{5}$ | ||
| C. | 6或$\frac{1-\sqrt{21}}{2}$ | D. | 6或-$\frac{9}{5}$或$\frac{1-\sqrt{21}}{2}$或$\frac{1+\sqrt{21}}{2}$ |
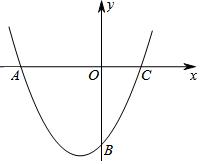 已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.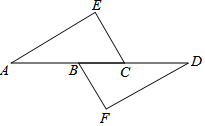 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.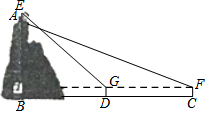 某综合实践活动小组实地测量了某山峰与中心广场的相对高度AB,其测量步骤如下:
某综合实践活动小组实地测量了某山峰与中心广场的相对高度AB,其测量步骤如下: