Question

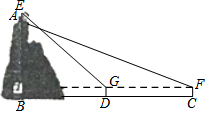
4．某综合实践活动小组实地测量了某山峰与中心广场的相对高度AB，其测量步骤如下：
（1）在中心广场的点C处安置侧倾器，测得此时山顶A的仰角∠AFH=22°；
（2）在点C与山脚B之间的D处安置侧倾器（C、D与B在同一直线上，且C、D之间的距离可以直接测得），测得此时山顶上凉亭顶部E的仰角∠EGH=45°；
（3）测得侧倾器的高度CF=DG=1.6米，并测得CD之间的距离为400米；
已知凉亭AE高度为10米，请根据测量数据求出该山峰与中心广场的相对高度AB．（结果保留整数）

Answer 1

分析 设AB=x，用x的代数式表示AH、FH，在Rt△AHF中，根据tan∠AFH=$\frac{AH}{HF}$，列出方程即可解决问题．

解答 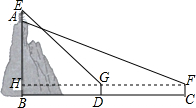解：设AB=x，由题意BH=DG=CF=1.6米，FG=CD=400米．
∴AH=（x-1.6）米，
∵∠EGH=45°，∠EHG=90°，
∴∠E=∠HGE=45°，
∴HE=HG=（x-1.6+10）米．
在Rt△AHF中，tan∠AFH=$\frac{AH}{HF}$，
∴tan22°=$\frac{x-1.6}{x-1.6+10+400}$，
∴0.4═$\frac{x-1.6}{x-1.6+10+400}$，
解得x≈275．
∴山峰与中心广场的相对高度AB约为275米．

点评 本题考查解直角三角形-仰角俯角问题，解题的关键是学会设未知数，利用三角函数构建方程解决问题，属于中考常考题型．