Question

以等腰三角形ABC的底边AB为直径作半圆O，分别交AC、BC于点D、E，若AB=10，∠OAE=30°，求DE的长．

Answer 1

考点：等边三角形的判定与性质

专题：

分析：分别连接AE、OE、OD，由条件可证明∠B=∠DAO=60°，可得∠DOE=60°，可知△ODE为等边三角形，则DE=OA=5．

解答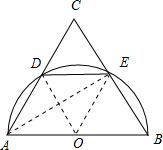：解：分别连接AE、OE、OD，
∵AB为直径，
∴∠AEB=90°，且∠OAE=30°，
∴∠B=60°，
∵AC=BC，
∴∠DAO=∠B=60°，
∴△OAD和△OBE均为等边三角形，
∴∠DOE=60°，
∴△DOE为等边三角形，
∴DE=OA=

1

2

AB=5．

点评：本题主要考查等腰三角形的性质及等边三角形的判定和性质，由条件得出∠DOE为60°是解题的关键．