题目内容
已知以点A(-1,-2)为顶点的抛物线与x轴交于B、C两点(点B在对称轴的左侧),BC=4.
(1)求以抛物线为图象的二次函数解析式;
(2)假设直线AO(O为坐标原点)与抛物线的另一个交点为D.求证:x轴是∠ABD的对称轴.
(1)求以抛物线为图象的二次函数解析式;
(2)假设直线AO(O为坐标原点)与抛物线的另一个交点为D.求证:x轴是∠ABD的对称轴.
考点:抛物线与x轴的交点
专题:
分析:(1)可设顶点式,由条件可知对称轴为x=-1,设对称轴交x轴于点E,且BC=4,可知BE=CE=2,可求得B,C两点的坐标,代入可求得解析式;
(2)可先求得直线AO的方程,联立抛物线方程可求得D点坐标,过D作DF⊥x轴,交x轴于点F,可知DF=BF,知∠DBC=45°,且AE=BE,则∠ABC=45°,可证得结论.
(2)可先求得直线AO的方程,联立抛物线方程可求得D点坐标,过D作DF⊥x轴,交x轴于点F,可知DF=BF,知∠DBC=45°,且AE=BE,则∠ABC=45°,可证得结论.
解答: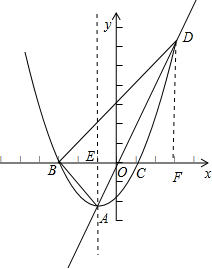 (1)解:因为顶点坐标为A(-1,2),所以其对称轴为x=-1,设对称轴交x轴于点E,如图,则BE=CE,且BC=4,
(1)解:因为顶点坐标为A(-1,2),所以其对称轴为x=-1,设对称轴交x轴于点E,如图,则BE=CE,且BC=4,
所以CE=2,可知C点坐标为(1,0),
设抛物线解析式为y=a(x+1)2-2,
把C点坐标代入可得:4a-2=0,解得a=
,
所以抛物线解析式为:y=
(x+1)2-2,
即y=
x2+x-
;
(2)证明:设直线AO的解析式为y=kx,代入A点坐标可得-2=-k,解得k=2,
所以直线AO的解析式为y=2x,
代入y=
x2+x-
可得2x=
x2+x-
,
解得x=-或3,所以D点坐标为(3,6),
如图,过D作DF⊥x轴,交x轴于点F,则DF=6,而OF=3,且BO=3,所以BF=DF,所以∠DBF=45°,
在Rt△ABE中,BE=2,AE=2,所以∠ABE=45°,
所以∠DBF=∠ABF,
所以x轴是∠ABD的对称轴.
 (1)解:因为顶点坐标为A(-1,2),所以其对称轴为x=-1,设对称轴交x轴于点E,如图,则BE=CE,且BC=4,
(1)解:因为顶点坐标为A(-1,2),所以其对称轴为x=-1,设对称轴交x轴于点E,如图,则BE=CE,且BC=4,所以CE=2,可知C点坐标为(1,0),
设抛物线解析式为y=a(x+1)2-2,
把C点坐标代入可得:4a-2=0,解得a=
| 1 |
| 2 |
所以抛物线解析式为:y=
| 1 |
| 2 |
即y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)证明:设直线AO的解析式为y=kx,代入A点坐标可得-2=-k,解得k=2,
所以直线AO的解析式为y=2x,
代入y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解得x=-或3,所以D点坐标为(3,6),
如图,过D作DF⊥x轴,交x轴于点F,则DF=6,而OF=3,且BO=3,所以BF=DF,所以∠DBF=45°,
在Rt△ABE中,BE=2,AE=2,所以∠ABE=45°,
所以∠DBF=∠ABF,
所以x轴是∠ABD的对称轴.
点评:本题主要考查待定系数法求函数解析式,已知抛物线的顶点时可设成顶点式,在证明x轴是∠ABD的对称轴是利用坐标得出线段的长再得出角相等是解题的关键.

练习册系列答案
相关题目
下列说法中,不正确的是( )
| A、3是(-3)2的算术平方根 |
| B、±3是(-3)的2平方根 |
| C、±3是(-3)2的算术平方根 |
| D、-3是(-3)3的立方根 |
下列各式从左到右正确的是( )
| A、-(-3x+2)=-3x+2 |
| B、-(2x-7)=2x+7 |
| C、-(-3x+2)=3x-2 |
| D、-(2x-7)=-2x-7 |