题目内容
20.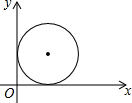 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )| A. | (4032π+1.0) | B. | (4032π+1.1) | C. | (4032π-1.0) | D. | (4032π-1.1) |
分析 由题意可知,该圆每向x轴正方向滚动1圈后,圆心的横坐标向右平移1个圆的周长,纵坐标不变,依此得出该圆向x轴正方向滚动2016圈后该圆的圆心坐标.
解答 解:∵圆的半径为1,
∴圆的周长为2π×1=2π,
∵图中圆的圆心坐标为(1,1),
∴该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),该圆的圆心横坐标为2016×2π=4032π,纵坐标为1,即(4032π+1,1).
故选B.
点评 本题考查了规律型:点的坐标,圆的周长公式,得出该圆每向x轴正方向滚动1圈后,圆心的横坐标向右平移1个圆的周长,纵坐标不变的规律是解题的关键.

练习册系列答案
相关题目
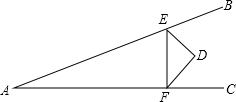 如图,∠BAC=30°,D在∠BAC内,E、F是AB、AC上动点,当△DEF周长最小时,求∠EDF的度数.
如图,∠BAC=30°,D在∠BAC内,E、F是AB、AC上动点,当△DEF周长最小时,求∠EDF的度数. 如图,AD,AC分别是⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,CD=3cm,求BO的长及劣弧CD的长.
如图,AD,AC分别是⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,CD=3cm,求BO的长及劣弧CD的长. 如图所示,∠ABC与∠ACB的内角平分线交于点O,∠ABC的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°,则∠BOC=120°,∠D=30°,∠E=60°.
如图所示,∠ABC与∠ACB的内角平分线交于点O,∠ABC的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°,则∠BOC=120°,∠D=30°,∠E=60°. 李大叔带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示.结合图形解答下列问题
李大叔带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示.结合图形解答下列问题