题目内容
9. 如图所示,∠ABC与∠ACB的内角平分线交于点O,∠ABC的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°,则∠BOC=120°,∠D=30°,∠E=60°.
如图所示,∠ABC与∠ACB的内角平分线交于点O,∠ABC的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°,则∠BOC=120°,∠D=30°,∠E=60°.
分析 根据角平分线的定义有∠ABC=2∠1,∠ACB=2∠2,根据三角形内角和定理得2∠2+2∠1+∠A=180°,即有∠2+∠1=90°-$\frac{1}{2}$∠A,再根据三角形内角和定理得到∠2+∠1+∠BOC=180°,于是有∠BOC=90°+$\frac{1}{2}$∠A,即可得到∠BOC的度数,三角形外角的性质有∠FCD=∠D+∠DBC,∠ACF=∠ABC+∠A,则2∠D+2∠DBC=∠ABC+∠A,即可得到∠D=$\frac{1}{2}$∠A,于是得到∠D,然后根据三角形的内角和即可得到结论.
解答 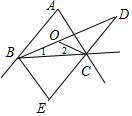 解:∵BO平分∠ABC,CO平分∠ACB,
解:∵BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠1,∠ACB=2∠2,
又∵∠ABC+∠ACB+∠A=180°,
∴2∠2+2∠1+∠A=180°,
∴∠2+∠1=90°-$\frac{1}{2}$∠A,
又∵∠2+∠1+∠BOC=180°,
∴90°-$\frac{1}{2}$∠A+∠BOC=180°,
∴∠BOC=90°+$\frac{1}{2}$∠A,
而∠A=50°,
∴∠BOC=90°+$\frac{1}{2}$×60°=120°,
∵∠DCF=∠D+∠DBC,∠ACF=∠ABC+∠A,BD平分∠ABC,DC平分∠ACF,
∴∠ACF=2∠DCF,∠ABC=2∠DBC,
∴2∠D+2∠DBC=∠ABC+∠A,
∴2∠D=∠A,即∠D=$\frac{1}{2}$∠A.
∵∠A=60°,
∴∠D=30°,
∵BE平分∠ABC相邻外角,BD平分∠ABC,
∴∠DBE=90°,
∴∠E=90°-∠D=60°,
故答案为:120°,30°60°.
点评 本题考查了角平分线定义,三角形内角和定理的应用,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
20.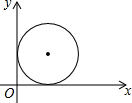 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )| A. | (4032π+1.0) | B. | (4032π+1.1) | C. | (4032π-1.0) | D. | (4032π-1.1) |
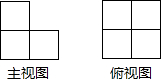 由若干个形状大小相同的小正方体木块组成的几何体的主视图和俯视图如下,则这样的小正方形木块至少有( )块.
由若干个形状大小相同的小正方体木块组成的几何体的主视图和俯视图如下,则这样的小正方形木块至少有( )块. 在所给的网格中建立适当的平面直角坐标系,在平面直角坐标系中描出下列各组点.(1,0),(6,0),(6,1),(5,0),(6,-1)
在所给的网格中建立适当的平面直角坐标系,在平面直角坐标系中描出下列各组点.(1,0),(6,0),(6,1),(5,0),(6,-1) 如图,在四边形ABCD中,AB=24,BC=20,CD=15,AD=7,∠C=90°,试求∠A的度数.
如图,在四边形ABCD中,AB=24,BC=20,CD=15,AD=7,∠C=90°,试求∠A的度数.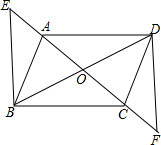 如图,四边形ABCD对角线交于点O,且O为AC中点,AE=CF,DF∥BE,求证:四边形ABCD是平行四边形.
如图,四边形ABCD对角线交于点O,且O为AC中点,AE=CF,DF∥BE,求证:四边形ABCD是平行四边形.