题目内容
10. 李大叔带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示.结合图形解答下列问题
李大叔带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示.结合图形解答下列问题(1)李大叔自带的零钱是多少?
(2)降价前他每千克土豆出售价是多少?
(3)降价后他按每千克0.4元将剩余土豆售完.这时他手中的钱(含备用零钱)是26元,则他一共带了多少千克土豆;
(4)请写出李大叔持有的钱与售出土豆数量的函数关系式?
分析 (1)由图象可知,当x=0时,y=5,所以农民自带的零钱是5元;
(2)可设降价前每千克土豆价格为k元,则可列出农民手中钱y与所售土豆千克数x之间的函数关系式,由图象知,当x=30时,y的值,从而求出这个函数式;
(3)可设降价后农民手中钱y与所售土豆千克数x之间的函数关系式,因为当x=a时,y=26,当x=30时,y=20,依此列出方程求解;
(4)由(2)当0≤x<30时y与x的函数关系式,由(3)可知当30≤x≤45时y与x的函数关系式.
解答 解:(1)由图象可知,当x=0时,y=5.
答:农民自带的零钱是5元.
(2)设降价前每千克土豆价格为k元,
则农民手中钱y与所售土豆千克数x之间的函数关系式为:y=kx+5,
∵当x=30时,y=20,
∴20=30k+5,
解得k=0.5.
答:降价前每千克土豆价格为0.5元.
(3)设降价后农民手中钱y与所售土豆千克数x之间的函数关系式为y=0.4x+b.
∵当x=a时,y=26,当x=30时,y=20,
∴0.4(a-30)+20=26,
解得a=45.
答:农民一共带了45千克土豆.
(4)由(2)当0≤x<30时,y=0.5x+5;
由(3)可知,将(30,2)代入y=0.4x+b,
得:12+b=20,解得:b=8,
故y=0.4x+8,
则:当0≤x<30时,y=0.5x+5;
当30≤x≤45时,y=0.4x+8.
点评 本题主要考查一次函数的应用,此类题目的解决需仔细分析函数图象,从中找寻信息,利用待定系数法求出函数解析式,从而解决问题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
20.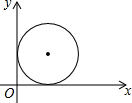 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )| A. | (4032π+1.0) | B. | (4032π+1.1) | C. | (4032π-1.0) | D. | (4032π-1.1) |
15.一元一次方程a1x2-2x+1=0的两根分别为x1,x2,一元二次方程a2x2-2x+1=0的两根为x3,x4,若0<x1<x3<x4<x2,则a1,a2的大小关系为( )
| A. | a1>a2 | B. | a1=a2 | C. | a1<a2 | D. | 大小无法确定 |
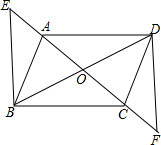 如图,四边形ABCD对角线交于点O,且O为AC中点,AE=CF,DF∥BE,求证:四边形ABCD是平行四边形.
如图,四边形ABCD对角线交于点O,且O为AC中点,AE=CF,DF∥BE,求证:四边形ABCD是平行四边形.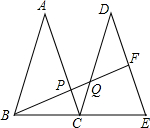 如图,△ABC和△DCE是两个全等的等腰三角形,底边BC、CE在一条直线上,F为DE的中点,连接BF,交AC于点P,交DC于点Q,则$\frac{PQ}{PB}$的值等于$\frac{1}{3}$.
如图,△ABC和△DCE是两个全等的等腰三角形,底边BC、CE在一条直线上,F为DE的中点,连接BF,交AC于点P,交DC于点Q,则$\frac{PQ}{PB}$的值等于$\frac{1}{3}$.