题目内容
5.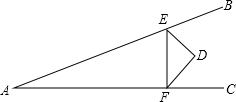 如图,∠BAC=30°,D在∠BAC内,E、F是AB、AC上动点,当△DEF周长最小时,求∠EDF的度数.
如图,∠BAC=30°,D在∠BAC内,E、F是AB、AC上动点,当△DEF周长最小时,求∠EDF的度数.
分析 欲使△DEF周长最小,只需点D、E、F三点共线即可.所以根据轴对称的性质找到点E、F;然后利用对顶角的性质,等量代换以及三角形内角和定理进行解答即可.
解答 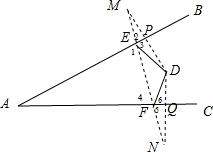 解:如图,过点D作关于直线AB对称的点M、关于直线AC对称的点N,连接MN,交AB于点E,交AC于点F,此时△DEF周长最小,
解:如图,过点D作关于直线AB对称的点M、关于直线AC对称的点N,连接MN,交AB于点E,交AC于点F,此时△DEF周长最小,
∵∠1=∠2,∠2=∠3,
∴∠1=∠3,同理∠4=∠6,
在△AEF中,∠1+∠4=180°-∠A=150°,∠3+∠6=150°,
∵∠MDE=90°-∠3,∠FDN=90°-∠6,
∴∠MDE+∠NDF=180°-(∠3+∠6)=30°,
∴∠PDQ=360°-90°-90°-30°=150°,
∴∠EDF=∠PDQ-(∠PDE-∠QDF)=150°-30°=120°.
点评 此题主要考查了轴对称最短路径问题,四边形的内角和,三角形的内角和,关键是确定E,F的位置.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列运算正确的是( )
| A. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B. | $\sqrt{4\frac{1}{9}}=2\frac{1}{3}$ | C. | $\sqrt{{{({2-\sqrt{5}})}^2}}=2-\sqrt{5}$ | D. | $\frac{1}{{2-\sqrt{3}}}=2+\sqrt{3}$ |
20.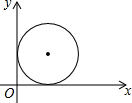 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )| A. | (4032π+1.0) | B. | (4032π+1.1) | C. | (4032π-1.0) | D. | (4032π-1.1) |
15.一元一次方程a1x2-2x+1=0的两根分别为x1,x2,一元二次方程a2x2-2x+1=0的两根为x3,x4,若0<x1<x3<x4<x2,则a1,a2的大小关系为( )
| A. | a1>a2 | B. | a1=a2 | C. | a1<a2 | D. | 大小无法确定 |
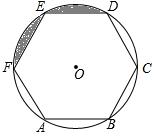 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1.
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1. 如图,在四边形ABCD中,AB=24,BC=20,CD=15,AD=7,∠C=90°,试求∠A的度数.
如图,在四边形ABCD中,AB=24,BC=20,CD=15,AD=7,∠C=90°,试求∠A的度数.