题目内容
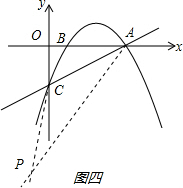
10.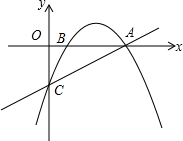 如图,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.
如图,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.(1)求抛物线的解析式;
(2)求抛物线与x轴的交点坐标;
(3)根据图象回答:
①当x取什么值时,y>0?②当x取什么值时,y的值随x的增大而减小?
(4)在这条抛物线上是否存在点P使以A、C、P为顶点的等腰三角形?若存在请写出符合条件的P点有多少个并写出其中一个点的坐标,若不存在请说明理由.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据抛物线上点的函数值为零时的点在x轴上,可得答案;
(3)①根据函数与不等式的关系,可得答案;
②根据y=ax2+bx+c,a<0时,对称轴的右侧y随x的增大而减小,可得答案;
(4)根据等腰三角形的定义,可得PA=PC,AC=AP,AC=CP,根据线段的垂直平分线,可得PD的解析式,根据解方程组,可得答案.
解答 解:(1)设过点A(4,0)、B(1,0)、C(0,-2)三点的解析式为:y=ax2+bx+c,
则$\left\{\begin{array}{l}{a×{4}^{2}+4b+c=0}\\{a×{1}^{2}+b+c=0}\\{c=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{5}{2}}\\{c=-2}\end{array}\right.$.
故抛物线的解析式为:y=$-\frac{1}{2}{x}^{2}+\frac{5}{2}x-2$.
(2)∵抛物线经过点A(4,0)、B(1,0),
∴抛物线与x轴的交点坐标为:(4,0),(1,0).
(3)①根据图象可知当函数图象在B和A之间时,函数图象在x轴上方.
∵点A(4,0)、B(1,0),
∴1<x<4时,y>0.
②由函数图象可知在对称轴的右侧时,y随x的增大而减小.
∵y=$-\frac{1}{2}{x}^{2}+\frac{5}{2}x-2$的顶点的横坐标为:x=$-\frac{\frac{5}{2}}{2×(-\frac{1}{2})}=\frac{5}{2}$,
∴x>$\frac{5}{2}$时,y随x的增大而减小.
(4)在这条抛物线上存在点P使以A、C、P为顶点的等腰三角形,符合条件的点P有四个,其中一个的坐标为P1($\frac{9+\sqrt{41}}{2}$,-6-$\sqrt{41}$).
如下图一、二、三、四所示: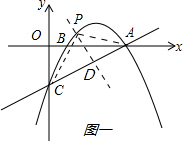
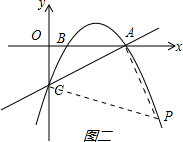
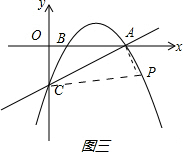
 ,
,
当AP=PC时,AC的解析式为y=$\frac{1}{2}$x-2,AC的中点D(2,-1),
PD⊥AC于D,设PD的解析式为y=-2x+b,
将D点坐标代入,得-4+b=1,解得b=3,
PD的解析式为y=-2x+3,
联立PD与抛物线,得
$\left\{\begin{array}{l}{y=-2x+3}\\{y=-\frac{1}{2}{x}^{2}+\frac{5}{2}x-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=\frac{9+\sqrt{41}}{2}}\\{{y}_{1}=-6-\sqrt{41}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{9-\sqrt{41}}{2}}\\{{y}_{2}=\sqrt{41}-6}\end{array}\right.$,
P1($\frac{9+\sqrt{41}}{2}$,-6-$\sqrt{41}$),P2($\frac{9-\sqrt{41}}{2}$,$\sqrt{41}$-6).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用函数值为零是抛物线与x轴的交点是解题关键,利用了函数与不等式的关系,二次函数的性质:a<0时,对称轴的右侧y随x的增大而减小;等腰三角形的判定,联立PD与抛物线得出方程组是解题关键.

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | 方程的解是x=m-6 | B. | m>6时,方程的解是正数 | ||
| C. | m<6时,方程的解为负数 | D. | 无法确定 |
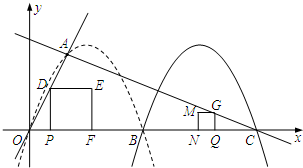 在平面直角坐标系中,抛物线y1=ax2+3x+c经过原点及点A(1,2),与x轴相交于另一点B.
在平面直角坐标系中,抛物线y1=ax2+3x+c经过原点及点A(1,2),与x轴相交于另一点B.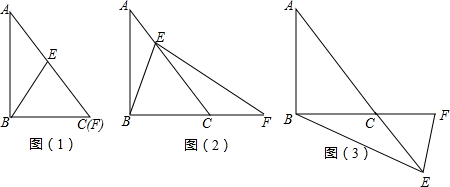
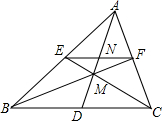 如图,E、F分别在△ABC的边AC、AB上,EF∥BC,BE与CF相交于M,AM交BC于D,交EF于N,求证:BD=DC.
如图,E、F分别在△ABC的边AC、AB上,EF∥BC,BE与CF相交于M,AM交BC于D,交EF于N,求证:BD=DC.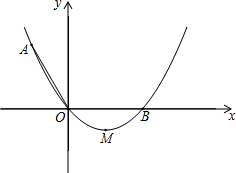 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,顶点为M且AO=0B=2,∠AOB=120°.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,顶点为M且AO=0B=2,∠AOB=120°.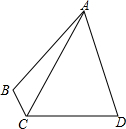 如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,AC=1,∠ACD=60°,求四边形ABCD的面积.
如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,AC=1,∠ACD=60°,求四边形ABCD的面积.