��Ŀ����
5��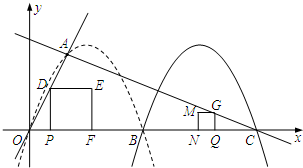 ��ƽ��ֱ������ϵ�У�������y1=ax2+3x+c����ԭ�㼰��A��1��2������x���ཻ����һ��B��
��ƽ��ֱ������ϵ�У�������y1=ax2+3x+c����ԭ�㼰��A��1��2������x���ཻ����һ��B����1����������y1�Ľ���ʽ��B�����ꣻ
��2������������y1��x=3Ϊ�Գ������ҷ��ۺõ�һ���µ�������y2����֪������y2��x�ύ�����㣬�����ұߵĽ���ΪC�㣮����P��O����������߶�OC��C���˶�����P����x��Ĵ��ߣ���ֱ��OA��D�㣬��PDΪ����PD���Ҳ���������PDEF��
�ٵ���E����������y1��ʱ����OP�ij���
������P���˶��ٶ�Ϊÿ��1����λ���ȣ�ͬʱ�߶�OC����һ��Q��C�������O���˶����ٶ�Ϊÿ��2����λ���ȣ���Q�㵽��O��ʱP��Q����ֹͣ�˶�����Q����x��Ĵ��ߣ���ֱ��AC����G�㣬��QGΪ����QG�������������QGMN���������������ηֱ���һ����ǡ������ͬһ��ֱ����ʱ����t��ֵ������������x���ϵı߳��⣩
���� ��1�����ö��κ���y1=ax2+3x+c��ͼ��ԭ�㼰��A��1��2�����ֱ�������a��c��ֵ��������ý���ʽ��Ȼ����y=0���ⷽ�̼������B�����ꣻ
��2���ٹ�A����AH��x����H�㣬����DP��AH���ó���OPD�ס�OHA���������OP�ij���
�ڷֱ����õ���F����N�غ�ʱ������F����Q�غ�ʱ������P����N�غ�ʱ������P����Q�غ�ʱ�����t��ֵ���ɣ�
���  �⣺��1����������y1=ax2+3x+c����ԭ�㼰��A��1��2����
�⣺��1����������y1=ax2+3x+c����ԭ�㼰��A��1��2����
��$\left\{\begin{array}{l}c=2\\ a+3+c=2\end{array}$ ���$\left\{\begin{array}{l}a=-1\\ c=0\end{array}$
��������y1�Ľ���ʽΪy1=-x2+3x��
��y1=0����-x2+3x=0�����x1=0��x2=3��
��B��3��0����
��2���������⣬�ɵ�C��6��0����
��ͼһ����A��AH��x����H����OP=a��
��DP��AH��
���ODP�ס�OAH��
��$\frac{DP}{OP}$=$\frac{AH}{OH}$=2��
��DP=2OP=2a��
��������PDEF����E��3a��2a����
��E��3a��2a����������y1=-x2+3x�ϣ�
��2a=-9a2+9a�����a1=0����ȥ����a2=$\frac{7}{9}$��
��OP�ij�Ϊ$\frac{7}{9}$��
����ֱ��AC�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}2=k+b\\ 0=6k+b\end{array}$ ���k=-$\frac{2}{5}$��b=$\frac{12}{5}$��
��ֱ��AC�Ľ���ʽΪy=-$\frac{2}{5}$x+$\frac{12}{5}$��
�����⣬OP=t��PF=2t��QC=2t��GQ=$\frac{4}{5}$t��
��ͼ1����EF��MN�غ�ʱ����OF+CN=6��
��3t+2t+$\frac{4}{5}$t=6��
��t=$\frac{30}{29}$��
��ͼ2����EF��GQ�غ�ʱ����OF+QC=6��
��3t+2t=6��
��t=$\frac{6}{5}$��
��ͼ3����DP��MN�غ�ʱ����OP+CN=6��
��t+2t+$\frac{4}{5}$t=6��
��t=$\frac{30}{19}$��
��ͼ4����DP��GQ�غ�ʱ����OP+CQ=6��
��t+2t=6��
��t=2��
���� ������Ҫ�����˶��κ������ۺ�Ӧ���Լ����������ε��ж��������Լ�����ϵ���������ʽ��������֪���ͼ��������۵ó�t��ֵ�ǽ���ؼ���

 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�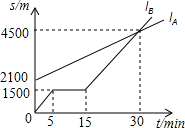 A��B����ͬѧ��һ��ѧУ��ѧ��Bͬѧ��ѧ��·�Ͼ���Aͬѧ�ң�Aͬѧ���У�Bͬѧ�����г���ij�죬A��B����ͬѧͬʱ�Ӽҳ�����ѧУ����ͼ��lA��ʾAͬѧ��Bͬѧ�ҵ�·��sA��m��������ʱ��t��min��֮��ĺ�����ϵͼ��lB��ʾBͬѧ��ҵ�·��sB��m��������ʱ��t��min��֮��ĺ�����ϵͼ��
A��B����ͬѧ��һ��ѧУ��ѧ��Bͬѧ��ѧ��·�Ͼ���Aͬѧ�ң�Aͬѧ���У�Bͬѧ�����г���ij�죬A��B����ͬѧͬʱ�Ӽҳ�����ѧУ����ͼ��lA��ʾAͬѧ��Bͬѧ�ҵ�·��sA��m��������ʱ��t��min��֮��ĺ�����ϵͼ��lB��ʾBͬѧ��ҵ�·��sB��m��������ʱ��t��min��֮��ĺ�����ϵͼ��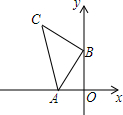 ��ͼ��A��-2��0����B��0��4������B��Ϊֱ�Ƕ����ڵڶ�����������ֱ�ǡ�ABC����C������Ϊ��-4��6����
��ͼ��A��-2��0����B��0��4������B��Ϊֱ�Ƕ����ڵڶ�����������ֱ�ǡ�ABC����C������Ϊ��-4��6����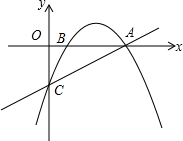 ��ͼ�������߾�����A��4��0����B��1��0����C��0��-2�����㣮
��ͼ�������߾�����A��4��0����B��1��0����C��0��-2�����㣮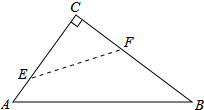 ��ͼ����Rt��ABC�У���C=90�㣬���ۡ�C��ʹ��C����б��AB��ijһ��D�����ۺ�ΪEF����E��F�ֱ��ڱ�AC��BC�ϣ������������жϣ�
��ͼ����Rt��ABC�У���C=90�㣬���ۡ�C��ʹ��C����б��AB��ijһ��D�����ۺ�ΪEF����E��F�ֱ��ڱ�AC��BC�ϣ������������жϣ�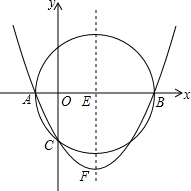 ��ͼ����֪��E��3��0��ΪԲ�ģ���5Ϊ�뾶�ġ�E��x�ύ��A��B���㣬��y�ύ��C�㣬������y=ax2+bx+c����A��B��C���㣬����ΪF��
��ͼ����֪��E��3��0��ΪԲ�ģ���5Ϊ�뾶�ġ�E��x�ύ��A��B���㣬��y�ύ��C�㣬������y=ax2+bx+c����A��B��C���㣬����ΪF��