题目内容
2.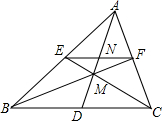 如图,E、F分别在△ABC的边AC、AB上,EF∥BC,BE与CF相交于M,AM交BC于D,交EF于N,求证:BD=DC.
如图,E、F分别在△ABC的边AC、AB上,EF∥BC,BE与CF相交于M,AM交BC于D,交EF于N,求证:BD=DC.
分析 根据EF∥BC,于是得到△AEN∽△ABD,△AFN∽△ACD,根据相似三角形的性质得到$\frac{EN}{BD}=\frac{AN}{AD}$,$\frac{NF}{CD}=\frac{AN}{AD}$,等量代换得到$\frac{EN}{BD}=\frac{FN}{CD}$,①同理得到$\frac{EN}{CD}=\frac{NF}{BD}$,②①÷②得,即可得到结论.
解答  证明:∵EF∥BC,
证明:∵EF∥BC,
∴△AEN∽△ABD,△AFN∽△ACD,
∴$\frac{EN}{BD}=\frac{AN}{AD}$,$\frac{NF}{CD}=\frac{AN}{AD}$,
∴$\frac{EN}{BD}=\frac{FN}{CD}$,①
∵EF∥BC,
∴△ENM∽△CDM,△NFM∽△BDM,
∴$\frac{EN}{CD}=\frac{NM}{DM}$,$\frac{NF}{BD}=\frac{MN}{MD}$,
∴$\frac{EN}{CD}=\frac{NF}{BD}$,②
①÷②得,
∴$\frac{CD}{BD}$=$\frac{BD}{CD}$,
∴CD2=BD2,
∴CD=BD.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=50°,则∠BDC=( )
如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=50°,则∠BDC=( )
 如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=50°,则∠BDC=( )
如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=50°,则∠BDC=( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
12.列方程解应用题:丰收村2台大收割机和5台小收割机同时工作2h共收割小麦3.6hm2;3台大收割机和2台小收割机同时工作5h共收割小麦8hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
11.若⊙O的直径为8,圆心到直线的距离d=8,则⊙O与直线的位置关系是( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 不确定 |
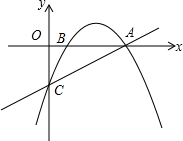 如图,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.
如图,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.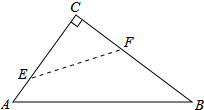 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上),给出以下判断:
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上),给出以下判断: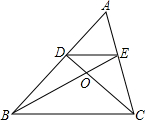 如图,已知点D、E分别在边AB、AC上,BE、CD交于点O,$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{EO}{BO}$.AC=5,EC=3,BC=6,BE=7
如图,已知点D、E分别在边AB、AC上,BE、CD交于点O,$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{EO}{BO}$.AC=5,EC=3,BC=6,BE=7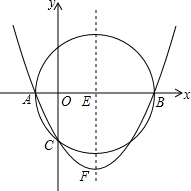 如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F.
如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F.