题目内容
20.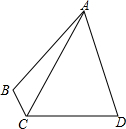 如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,AC=1,∠ACD=60°,求四边形ABCD的面积.
如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,AC=1,∠ACD=60°,求四边形ABCD的面积.
分析 延长CD到E,使DE=BC,连接AE,过点A作AF⊥CD于点F,根据SAS可证明△ABC≌△ADE,得出AC=AE,再证明△ACE是等边三角形,求出高AF的值,由△ABC≌△ADE,得到S四边形ABCD=S△ACE=即可解答.
解答 解:如图,延长CD到E,使DE=BC,连接AE,过点A作AF⊥CD于点F,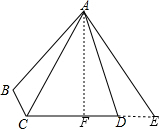
∵∠B+∠ADC=180°,∠ADE+∠ADC=180°,
∴∠B=∠ADE,
在△ABC和△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠ADE}\\{BC=DE}\end{array}\right.$,
∴△ABC≌△ADE(SAS),
∴AC=AE=1,∠BAC=∠DAE,
∵∠CAE=∠CAD+∠DAE=∠CAD+∠BAC=∠BAD=60°,
∴△ACE是等边三角形,
∵∠ACD=60°,
∴AF=AC•sin60°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
∴S四边形ABCD=S△ACE=$\frac{1}{2}×1×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是作出辅助线,证明△ABC≌△ADE.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
11.若⊙O的直径为8,圆心到直线的距离d=8,则⊙O与直线的位置关系是( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 不确定 |
 如图,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.
如图,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.
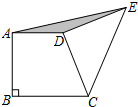 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=6.以D为直角顶点CD为腰向外作等腰Rt△CDE,连接AE,则△ADE的面积是4.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=6.以D为直角顶点CD为腰向外作等腰Rt△CDE,连接AE,则△ADE的面积是4.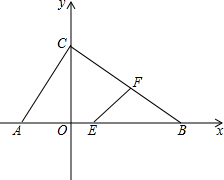 如图,在平面直角坐标系中,△ABC的顶点都在坐标轴上,OA=2,OC=3,OB=4.点E,F分别是线段AB,BC上的动点(不与端点A,B重合),点E从点A出发沿x轴正方向以每秒2个单位长度的速度向点B运动,同时点F从点B出发沿线段BC方向以每秒1个单位长度的速度向点C运动(当点E停止时,点F也同时停止),当两个动点运动了t秒时,解答下列问题:
如图,在平面直角坐标系中,△ABC的顶点都在坐标轴上,OA=2,OC=3,OB=4.点E,F分别是线段AB,BC上的动点(不与端点A,B重合),点E从点A出发沿x轴正方向以每秒2个单位长度的速度向点B运动,同时点F从点B出发沿线段BC方向以每秒1个单位长度的速度向点C运动(当点E停止时,点F也同时停止),当两个动点运动了t秒时,解答下列问题: