题目内容
5.下列代数式中:$-m,{a^2}+a,-x-3,\frac{b}{a},\frac{a+b}{2},-2\frac{1}{2},\sqrt{2}x,\root{3}{a}$.属于单项式的有:$-m,-2\frac{1}{2},\sqrt{2}x,\root{3}{a}$;
属于多项式的有:${a^2}+a,-x-3,\frac{a+b}{2}$.
分析 根据单项式、多项式、立方根,即可解答.
解答 解:属于单项式的有:$-m,-2\frac{1}{2},\sqrt{2}x,\root{3}{a}$;
属于多项式的有:${a^2}+a,-x-3,\frac{a+b}{2}$;
故答案为:$-m,-2\frac{1}{2},\sqrt{2}x,\root{3}{a}$;${a^2}+a,-x-3,\frac{a+b}{2}$.
点评 本题考查了单项式、多项式、立方根,解决本题的关键是熟记单项式、多项式、立方根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.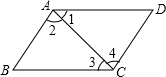 如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
 如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )| A. | ∠1=∠3 | B. | ∠B+∠BCD=180° | C. | ∠2=∠4 | D. | ∠D+∠BAD=180° |
15.已知a2=25,$\sqrt{{b}^{2}}$=7,且|a+b|=a+b,则a-b的值为( )
| A. | 2或12 | B. | 2或-12 | C. | -2或12 | D. | -2或-12 |
 如图,射线BD是∠MBN的平分线,点A、C分别是角的两边BM、BN上两点,且AB=BC,E是线段BC上一点,线段EC的垂直平分线交射线BD于点F,连结AE交BD于点G,连结AF、EF、FC.
如图,射线BD是∠MBN的平分线,点A、C分别是角的两边BM、BN上两点,且AB=BC,E是线段BC上一点,线段EC的垂直平分线交射线BD于点F,连结AE交BD于点G,连结AF、EF、FC. 某处欲建一观景平台,如图所示,原设计平台的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°,则调整后楼梯AD的长为6$\sqrt{2}$m.(结果保留根号)
某处欲建一观景平台,如图所示,原设计平台的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°,则调整后楼梯AD的长为6$\sqrt{2}$m.(结果保留根号)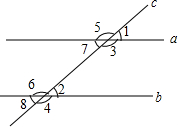 如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )
如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )