题目内容
15. 如图,射线BD是∠MBN的平分线,点A、C分别是角的两边BM、BN上两点,且AB=BC,E是线段BC上一点,线段EC的垂直平分线交射线BD于点F,连结AE交BD于点G,连结AF、EF、FC.
如图,射线BD是∠MBN的平分线,点A、C分别是角的两边BM、BN上两点,且AB=BC,E是线段BC上一点,线段EC的垂直平分线交射线BD于点F,连结AE交BD于点G,连结AF、EF、FC.(1)求证:AF=EF;
(2)求证:△AGF∽△BAF;
(3)若点P是线段AG上一点,连结BP,若∠PBG=$\frac{1}{2}$∠BAF,AB=3,AF=2,求$\frac{EG}{GP}$.
分析 (1)由于EF=CF,要证AF=EF,只需证FA=FC,只需证△ABF≌△CBF即可;
(2)由于∠AFG=∠BFA,要证△AGF∽△BAF,只需证∠FAE=∠ABF,易得∠FAE=∠FEA,∠ABF=∠CBF,只需证∠ABC+∠AFE=180°,只需证∠BAF+∠BEF=180°,只需证到∠BAF=∠FEC即可;
(3)由△AGF∽△BAF可得∠BAF=∠AGF,$\frac{FG}{AG}$=$\frac{AF}{AB}$=$\frac{2}{3}$,易证△BGE∽△AGF,则有$\frac{GE}{BG}$=$\frac{GF}{AG}$=$\frac{2}{3}$,由条件∠PBG=$\frac{1}{2}$∠BAF可得∠PBG=$\frac{1}{2}$∠AGF,由此可得∠BPG=∠PBG,即可得到BG=PG,问题得以解决.
解答 解:(1)∵BF平分∠ABC,
∴∠ABF=∠CBF.
在△ABF和△CBF中,
$\left\{\begin{array}{l}{BA=BC}\\{∠ABF=∠CBF}\\{BF=BF}\end{array}\right.$,
∴△ABF≌△CBF,
∴AF=CF.
∵点F在EC的垂直平分线上,
∴EF=CF,
∴AF=EF;
(2)∵△ABF≌△CBF,
∴∠BAF=∠BCF.
∵FE=FC,
∴∠FEC=∠FCE,
∴∠BAF=∠FEC.
∵∠BEF+∠FEC=180°,
∴∠BAF+∠BEF=180°.
∵∠BAF+∠ABE+∠BEF+∠AFE=360°,
∴∠ABE+∠AFE=180°.
∵FA=FE,
∴∠FAE=∠FEA.
∵∠AFE+∠FAE+∠FEA=180°,
∴∠ABE=∠FAE+∠FEA=2∠FAE.
又∵∠ABE=2∠ABF,
∴∠FAE=∠ABF.
∵∠AFG=∠BFA,
∴△AGF∽△BAF;
(3)∵△AGF∽△BAF,
∴∠AGF=∠BAF,$\frac{FG}{FA}$=$\frac{AG}{BA}$.
∵∠PBG=$\frac{1}{2}$∠BAF,AB=3,AF=2,
∴∠PBG=$\frac{1}{2}$∠AGF,$\frac{FG}{2}$=$\frac{AG}{3}$,
∴∠BPG=∠PBG,$\frac{FG}{AG}$=$\frac{2}{3}$,
∴PG=BG,
∴$\frac{EG}{PG}$=$\frac{EG}{BG}$.
∵∠GAF=∠ABF=∠EBF,∠AGF=∠BGE,
∴△BGE∽△AGF,
∴$\frac{GE}{BG}$=$\frac{GF}{AG}$=$\frac{2}{3}$,
∴$\frac{EG}{PG}$=$\frac{2}{3}$.
点评 本题主要考查了全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形的判定与性质、线段垂直平分线的性质、多边形的内角和定理、三角形的外角性质等知识,证到∠ABE+∠AFE=180°是解决第(2)小题的关键,证到BG=PG是解决第(3)小题的关键.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | -24a8b4 | B. | -24a9b4 | C. | 24a8b4 | D. | 24a9b7 |
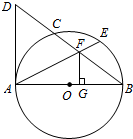 如图,AB是⊙O的直径,BD交⊙O于点C,E为 BC 的中点,连接AE交BD于点F,作FG⊥AB,垂足为G,连接AD,且∠D=2∠BAE.
如图,AB是⊙O的直径,BD交⊙O于点C,E为 BC 的中点,连接AE交BD于点F,作FG⊥AB,垂足为G,连接AD,且∠D=2∠BAE. 
 如图所示的圆柱体中底面圆的半径是$\frac{4}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是4$\sqrt{2}$.
如图所示的圆柱体中底面圆的半径是$\frac{4}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是4$\sqrt{2}$.
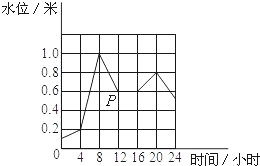 近一个月来某地区遭受暴雨袭击,水位上涨,小明以警戒水位为0点,用折线图表示某一天河水水位的情况,如图所示,请你结合图形判断下列叙述不正确的个数( )
近一个月来某地区遭受暴雨袭击,水位上涨,小明以警戒水位为0点,用折线图表示某一天河水水位的情况,如图所示,请你结合图形判断下列叙述不正确的个数( )