题目内容
2.若y是x的一次函数,图象过点(-3,2),且与直线y=4x+6交于x轴上一点,求此函数的解析式.分析 先根据x轴上点的坐标特征求出直线y=2x+6与x轴的交点坐标为(-3,0),然后利用待定系数法求一次函数解析式.
解答 解:当y=0时,4x+6=0,解得x=-$\frac{3}{2}$,则直线y=4x+6与x轴的交点坐标为(-$\frac{3}{2}$,0),
设一次函数解析式为y=kx+b,
把(-3,2),(-$\frac{3}{2}$,0)代入得$\left\{\begin{array}{l}{-3k+b=2}\\{-\frac{3}{2}k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-2}\end{array}\right.$,
所以所求函数解析式为y=-$\frac{4}{3}$x-2.
点评 本题考查了两条直线相交或平行的问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
17.x>-y,则下列不等式中成立的有( )
| A. | x+y<0 | B. | x-y>0 | C. | a2x>-a2y | D. | 3x+3y>0 |
7. 如图,已知l1∥l2,且∠1=120°,则∠2=( )
如图,已知l1∥l2,且∠1=120°,则∠2=( )
 如图,已知l1∥l2,且∠1=120°,则∠2=( )
如图,已知l1∥l2,且∠1=120°,则∠2=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
 在△ABC中,CE、DF分别垂直于AB,点E、F分别为垂足,AC∥DE,CE平分∠ACB.求证:∠EDF=∠BDF.
在△ABC中,CE、DF分别垂直于AB,点E、F分别为垂足,AC∥DE,CE平分∠ACB.求证:∠EDF=∠BDF.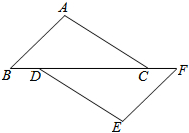 如图,点B、D、C、F在同一直线上,且BD=FC,AB=EF.请你在横线上添加一个条件:∠B=∠ACB(不再添加辅助线),使△ABC≌△EFD,并说明理由.
如图,点B、D、C、F在同一直线上,且BD=FC,AB=EF.请你在横线上添加一个条件:∠B=∠ACB(不再添加辅助线),使△ABC≌△EFD,并说明理由. 如图,已知AB=AC,B是AD中点,E是AB中点,求证:CD=2CE.
如图,已知AB=AC,B是AD中点,E是AB中点,求证:CD=2CE.