题目内容
14.下列各数中互为相反数的是( )| A. | $({-\frac{2}{3}})$和$-\frac{2}{3}$ | B. | $({-\frac{2}{3}})$和$-\frac{3}{2}$ | C. | $({-\frac{2}{3}})$和$\frac{2}{3}$ | D. | $({-\frac{2}{3}})$和$\frac{3}{2}$ |
分析 只有符号不同的数互为相反数,据此判断即可.
解答 解:A、两个数相同,不是相反数,不符合题意;
B、两个数的绝对值不同,不是互为相反数,不符合题意;
C、两个数的绝对值相同,是互为相反数,符合题意;
D、两个数的绝对值不同,不是互为相反数,不符合题意.
故选C.
点评 本题考查了相反数的概念,解题的关键是注意:两个数符号不同,但是绝对值相等,就是互为相反数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.一个口袋里装有除颜色外,形状、大小,质量均相同的若干个小球,其中红球1个,白球有3个,黑球有6个,甲、乙、丙三位同学分别做同一实验:把口袋里的球搅匀后,摸出一个球来,记下颜色后,将球放回袋中,再次重复,共进行10次,下表是记录的结果:
(1)请把甲、乙两位同学的记录补充完整;
(2)如果你是丙同学,请把你的实验结果填写完整;
(3)比较每位同学的实验结果,哪位同学摸出红球的可能性最大?哪位同学摸出黑球的可能性最大?
(4)三位同学所做的实验中,事件“摸到红球”的可能性,事件“摸到白球”的可能性,事件“摸到黑球”的可能性分别是多少,这三个事件的可能性之和是多少?
| 同学 | 红球 | 白球 | 黑球 |
| 甲 | 1 | 5 | |
| 乙 | 3 | 7 | |
| 丙 |
(2)如果你是丙同学,请把你的实验结果填写完整;
(3)比较每位同学的实验结果,哪位同学摸出红球的可能性最大?哪位同学摸出黑球的可能性最大?
(4)三位同学所做的实验中,事件“摸到红球”的可能性,事件“摸到白球”的可能性,事件“摸到黑球”的可能性分别是多少,这三个事件的可能性之和是多少?
6.下列各组数中,数值相等的是( )
| A. | (-2)3与-23 | B. | 23与32 | C. | (-3)2与-32 | D. | -(-2)与-|-2| |
3.以下列各组线段为边,不能构成三角形的是( )
| A. | $\sqrt{2}$,$\sqrt{3}$,1 | B. | 3,4,5 | C. | 2,7,9 | D. | $\frac{3}{2}$,3,$\frac{5}{2}$ |
4.已知点P1(n-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2005的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | (-3)2005 |
 蔬菜大棚的支架是抛物线型,跨度是8m,内侧距离地面高度相等处各有一螺栓,螺栓之间的水平距离为6m,请建立适当的直角坐标系,写出这段抛物线所对应的二次函数的表达式,并求出支架最高点距地面的距离(精确到0.1m)
蔬菜大棚的支架是抛物线型,跨度是8m,内侧距离地面高度相等处各有一螺栓,螺栓之间的水平距离为6m,请建立适当的直角坐标系,写出这段抛物线所对应的二次函数的表达式,并求出支架最高点距地面的距离(精确到0.1m)
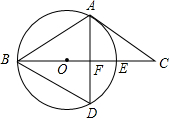 如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,点D在⊙O上,BD=BA,∠DAC=2∠ABC,⊙O交BC于点E,AD交BC于点F.
如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,点D在⊙O上,BD=BA,∠DAC=2∠ABC,⊙O交BC于点E,AD交BC于点F.