题目内容
19.一个口袋里装有除颜色外,形状、大小,质量均相同的若干个小球,其中红球1个,白球有3个,黑球有6个,甲、乙、丙三位同学分别做同一实验:把口袋里的球搅匀后,摸出一个球来,记下颜色后,将球放回袋中,再次重复,共进行10次,下表是记录的结果:| 同学 | 红球 | 白球 | 黑球 |
| 甲 | 1 | 5 | |
| 乙 | 3 | 7 | |
| 丙 |
(2)如果你是丙同学,请把你的实验结果填写完整;
(3)比较每位同学的实验结果,哪位同学摸出红球的可能性最大?哪位同学摸出黑球的可能性最大?
(4)三位同学所做的实验中,事件“摸到红球”的可能性,事件“摸到白球”的可能性,事件“摸到黑球”的可能性分别是多少,这三个事件的可能性之和是多少?
分析 (1)根据摸球的次数为10,即可把甲、乙两位同学的记录补充完整;
(2)根据黑球的数量最多,白球的数量次之,红球的数量最少即可把丙同学的记录表补充完整;
(3)根据(1),(2)中的答案即可做出回答;
(4)由概率公式分别计算即可求出各自的概率,进而可求出其概率之和.
解答 解:(1)∵摸球10次,红球,黑球分别出现了1和5次,
∴甲中的白球出现的次数为10-1-5=4次,
∵摸球10次,白球,黑球分别出现了3和7次,
∴乙中的红球出现的次数为10-3-7=0次;
故答案为4,0;
(2)∵红球1个,白球有3个,黑球有6个,
∴丙同学的实验结果可以为2,3,5;
(3)由(1),(2)中的数据可知丙学摸出红球的可能性最大,甲同学摸出黑球的可能性最大;
(4)三位同学所做的实验中,事件“摸到红球”的可能性,事件“摸到白球”的可能性,事件“摸到黑球”的可能性分别是$\frac{1}{10}$,$\frac{2}{5}$,$\frac{1}{2}$;0,$\frac{3}{10}$,$\frac{7}{10}$;$\frac{1}{5}$,$\frac{3}{10}$,$\frac{1}{2}$;
这三个事件的可能性之和是1.
点评 本题考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:概率=所求情况数与总情况数之比.部分数目=总体数目乘以相应概率,解题的关键是熟记概率公式,并且能够熟练运用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
14.下列各数中互为相反数的是( )
| A. | $({-\frac{2}{3}})$和$-\frac{2}{3}$ | B. | $({-\frac{2}{3}})$和$-\frac{3}{2}$ | C. | $({-\frac{2}{3}})$和$\frac{2}{3}$ | D. | $({-\frac{2}{3}})$和$\frac{3}{2}$ |
 如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是65°.
如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是65°.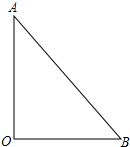 如图所示,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.
如图所示,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.