题目内容
5. 如图,每个小正方形的边长均为1,△ABC和△DEC的顶点均在“格点”上,则$\frac{△DEC周长}{△ABC周长}$=( )
如图,每个小正方形的边长均为1,△ABC和△DEC的顶点均在“格点”上,则$\frac{△DEC周长}{△ABC周长}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
分析 根据勾股定理求出两个三角形的各个边的长度,代入即可求出答案.
解答 解:∵每个小正方形的边长均为1,
∴由勾股定理得:AC=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,BC=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$,
DC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,CE=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,DE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴$\frac{△DEC的周长}{△ABC的周长}$=$\frac{AC+AB+BC}{DC+CE+DE}$=$\frac{1}{2}$,
故选A.
点评 本题考查了勾股定理,相似三角形的性质和判定的应用,能求出各个边的长度是解此题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
13. 如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
 如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )| A. | 0,1,-2 | B. | 1,0,-2 | C. | -2,0,1 | D. | 0,-2,1 |
20.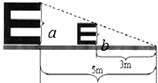 根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )
根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )
 根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )
根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )| A. | 1.44cm | B. | 2.16cm | C. | 2.4cm | D. | 3.6cm |
15.若分式$\frac{x-1}{x-3}$有意义,则x满足的条件是( )
| A. | x=1 | B. | x=3 | C. | x≠1 | D. | x≠3 |
 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2),点B的坐标为(-4,5),点C的坐标为(-5,3).
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2),点B的坐标为(-4,5),点C的坐标为(-5,3).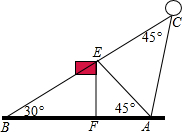 如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.
如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.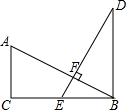 如图,已知AC⊥CB,DB⊥CB,AB⊥DE,垂足为F,AB=DE,E是BC的中点.
如图,已知AC⊥CB,DB⊥CB,AB⊥DE,垂足为F,AB=DE,E是BC的中点.