题目内容
20.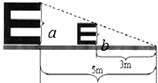 根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )
根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )| A. | 1.44cm | B. | 2.16cm | C. | 2.4cm | D. | 3.6cm |
分析 如图,易得△OAB∽△OCD,利用它们对应边成比例,即可得到题目的结论.
解答  解:如图,依题意得△OAB∽△OCD
解:如图,依题意得△OAB∽△OCD
则$\frac{DC}{AB}$=$\frac{DO}{BO}$,
即$\frac{3.6}{b}$=$\frac{5}{3}$,
解得:b=2.16.
故选:B.
点评 此题主要考查了相似三角形的应用,利用相似三角形的性质解题是解题关键.

练习册系列答案
相关题目
8. 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )
 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )| A. | 70° | B. | 90° | C. | 110° | D. | 120° |
15.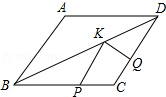 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
5. 如图,每个小正方形的边长均为1,△ABC和△DEC的顶点均在“格点”上,则$\frac{△DEC周长}{△ABC周长}$=( )
如图,每个小正方形的边长均为1,△ABC和△DEC的顶点均在“格点”上,则$\frac{△DEC周长}{△ABC周长}$=( )
 如图,每个小正方形的边长均为1,△ABC和△DEC的顶点均在“格点”上,则$\frac{△DEC周长}{△ABC周长}$=( )
如图,每个小正方形的边长均为1,△ABC和△DEC的顶点均在“格点”上,则$\frac{△DEC周长}{△ABC周长}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
12.下列说法:①三点确定一个圆;②平分弦的直径必垂直于这条弦;③圆周角等于圆心角的一半;④等弧所对的圆心角相等;⑤各角相等的圆内接多边形是正多边形.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价和售价如下表:
(1)求甲,乙两种节能灯各进货多少时,使进货款恰好为46 000元;
(2)应如何进货,使销售完节能灯时,商场获得的利润恰好是进货价的30%,此时利润为多少?
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(2)应如何进货,使销售完节能灯时,商场获得的利润恰好是进货价的30%,此时利润为多少?
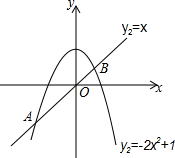 如图,抛物线y1=-2x2+1和直线y2=x交于A、B两点.
如图,抛物线y1=-2x2+1和直线y2=x交于A、B两点.