��Ŀ����
18����ͼ����ƽ��ֱ������ϵxOy�У�����y=-x��ͼ��l�ǵڶ��������Ľ�ƽ���ߣ���1��ʵ����̽������ͼ�۲���֪A��-1��3������ֱ��l�ĶԳƵ�A�������Ϊ��-3��1��������д����B��5��3������ֱ��l�ĶԳƵ�B�������Ϊ��-3��-5����
��2�������뷢�֣����ͼ�Σ��Լ�ѡ������һ�ԣ�ͨ���۲������꣬��ᷢ�֣�����ƽ������һ��P��m��n�����ڵڶ��������Ľ�ƽ����l�ĶԳƵ�P�������Ϊ��-n��-m����
��3���������ع㣺
����֪����C��6��0����D��2��4��������ֱ��l��ȷ��һ��P��ʹ��P��C��D����ľ���֮����С����ͼ�л�����P��λ�ã�������ͼ�ۼ����������P�����꣮
���ڢٵ������£������PC+PD����Сֵ��
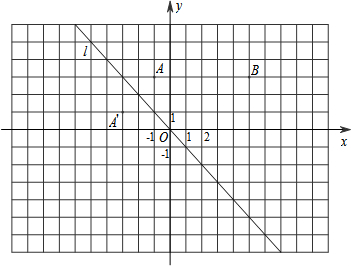
���� ��1���۲�ͼ�εó���B��5��3������ֱ��l�ĶԳƵ�B������꼴�ɣ�
��2�������ܽ�õ�һ���Թ��ɣ�д��P��m��n�����ڵڶ��������Ľ�ƽ����l�ĶԳƵ�P������꼴�ɣ�
��3������ͼ������C����ֱ�� l �ĶԳƵ�C�䣬����C��D����l�ڵ�P������CP������ͼ��֪��PC=PC�䣬�����õ�PC+PD=C��D�������ʱP���꼴�ɣ������ù��ɶ������PC+PD����Сֵ���ɣ�
��� �⣺��1����������ã�B�䣨-3��-5����
��2����������ã�P�䣨-n��-m����
�ʴ�Ϊ����1����-3��-5������2����-n��-m����
��3������ͼ������C����ֱ�� l �ĶԳƵ�C�䣬����C��D����l�ڵ�P������CP��
����ͼ��֪��PC=PC�䣬
��PC+PD=PC��+PD=C��D��
���P����
��C��6��0����
��C�䣨0��-6����
��ֱ��C��D�Ľ���ʽΪy=kx-6��
��D��2��4����
��k=5��
��ֱ��C��D�Ľ���ʽΪy=5x-6��
��$\left\{\begin{array}{l}{y=5x-6}\\{y=-x}\end{array}\right.$ ��$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$��
��P��1��-1����
��PC+PD=$\sqrt{{2}^{2}+1{0}^{2}}$=2$\sqrt{26}$��
���� ��������һ�κ����ۺ��⣬�漰��֪ʶ�У��ԳƵ����ʣ����ɶ�����һ�κ��������ʣ�Ū���������y=-x�ԳƵ����������ϵ�ǽⱾ��Ĺؼ���

 ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д� �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д� �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д�| A�� | ͬλ����� | B�� | �ڴ������ | ||
| C�� | ͬ���ڽ���� | D�� | ���͵�����ֱ��ƽ�� |
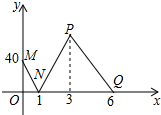 ��һ���ϱ�����ĺ�����������A��B��C�����ۿڣ�һ���ִ��Ӹۿ�A���������ٺ��е��ۿ�C�ص��ۿ�B���ִ���ۿ�B�ľ���y��ǧ�ף��뺽��ʱ��x��Сʱ��֮��ĺ���ͼ����ͼ�е�����MN-NP-PQ��ʾ����֪�˴κ��й�����ˮ���ٶȺ��ִ��ľ�ˮ�ٶȱ��ֲ��䣮
��һ���ϱ�����ĺ�����������A��B��C�����ۿڣ�һ���ִ��Ӹۿ�A���������ٺ��е��ۿ�C�ص��ۿ�B���ִ���ۿ�B�ľ���y��ǧ�ף��뺽��ʱ��x��Сʱ��֮��ĺ���ͼ����ͼ�е�����MN-NP-PQ��ʾ����֪�˴κ��й�����ˮ���ٶȺ��ִ��ľ�ˮ�ٶȱ��ֲ��䣮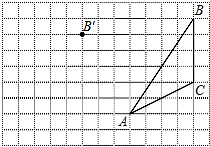 ��ͼ����գ���ͼ������ֽ��ÿ��С�����εı߳���Ϊ1���ڷ���ֽ�ڽ���ABC����һ��ƽ�ƺ�õ���A��B��C�䣬ͼ�б���˵�B�Ķ�Ӧ��B�䣮
��ͼ����գ���ͼ������ֽ��ÿ��С�����εı߳���Ϊ1���ڷ���ֽ�ڽ���ABC����һ��ƽ�ƺ�õ���A��B��C�䣬ͼ�б���˵�B�Ķ�Ӧ��B�䣮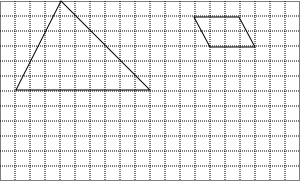 ��ͼ��ÿ��С�����εı߳�����1
��ͼ��ÿ��С�����εı߳�����1