题目内容
若|a+
|+(b-2)2=0,则(ab)2015= .
| 1 |
| 2 |
考点:非负数的性质:偶次方,非负数的性质:绝对值
专题:
分析:根据非负数的性质可求出a、b的值,再将它们代入(ab)2015中求解即可.
解答:解:∵|a+
|+(b-2)2=0,
∴a+
=0,b-2=0;
a=-
,b=2;
则(ab)2015=(-
×2)2015=-1.
故答案为-1.
| 1 |
| 2 |
∴a+
| 1 |
| 2 |
a=-
| 1 |
| 2 |
则(ab)2015=(-
| 1 |
| 2 |
故答案为-1.
点评:本题考查了非负数的性质:有限个非负数的和为零,那么每一个加数也必为零.

练习册系列答案
相关题目
依依买了7本数学书和2本语文书共花了100元;菲菲买了4本语文书和2本数学书共花了80元.则买3本数学书要花( )元.
| A、30 | B、20 | C、15 | D、45 |
若x+
=3,则
的值是( )
| 1 |
| x |
| x |
| x2+x+1 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知a与b互为相反数,且b≠0,下列各式不成立的是( )
| A、a+b=0 | ||
| B、a2=b2 | ||
| C、|a|=-|b| | ||
D、
|
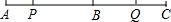 如图所示,线段AC上有一点B,且AB=40cm,BC=30cm,点P从A点出发,沿AC方向以3cm/秒的速度匀速向C点运动,点Q从C点出发,沿CA方向以a cm/秒的速度匀速向A点运动,两点同时出发(P、Q只在线段AC上运动).
如图所示,线段AC上有一点B,且AB=40cm,BC=30cm,点P从A点出发,沿AC方向以3cm/秒的速度匀速向C点运动,点Q从C点出发,沿CA方向以a cm/秒的速度匀速向A点运动,两点同时出发(P、Q只在线段AC上运动).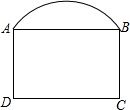 如图,工厂大门由弧线AB和矩形ABCD组成,
如图,工厂大门由弧线AB和矩形ABCD组成,