题目内容
8.若点A(m,y1),B(m+1,y2)都在二次函数y=ax2+4ax+2(a>0)的图象上,且y1<y2,则m的取值范围是( )| A. | m>-$\frac{5}{2}$ | B. | m≥-2 | C. | m<-1 | D. | m≤-3 |
分析 根据二次函数的解析式可得出二次函数的对称轴为x=-2,结合二次项系数大于0,可找出函数的单调区间,再结合A、B点坐标的特点即可得出关于m的一元一次不等式,解不等式即可得出结论.
解答 解:二次函数y=ax2+4ax+2(a>0)的对称轴为x=-$\frac{4a}{2a}$=-2,
∵a>0,
∴二次函数图象在x<-2上单调递减,在x≥-2上单调递增.
∵点A(m,y1),B(m+1,y2)都在二次函数y=ax2+4ax+2(a>0)的图象上,且y1<y2,
∴m+m+1>-2×2,解得:m>-$\frac{5}{2}$.
故选A.
点评 本题考查了二次函数图象上点的坐标特征,解题的关键是根据二次函数的性质找出关于m的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据二次函数的性质结合二次函数的对称轴找出关于点的横坐标之和的不等式是关键.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
13.一个等腰三角形的两条边长分别3和6,则该等腰三角形的周长是( )
| A. | 12 | B. | 13 | C. | 15 | D. | 12或15 |
 如图,AB是⊙O直径,CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则S阴影=$\frac{2π}{3}$.
如图,AB是⊙O直径,CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则S阴影=$\frac{2π}{3}$.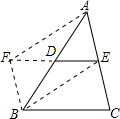 完成下列证明过程,求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
完成下列证明过程,求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.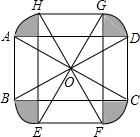 如图,将矩形ABCD绕对角线的交点0逆时针旋转90°得到矩形EFGH,已知AB=2,BC=2$\sqrt{3}$,则由旋转得到的阴影部分的面积为$\frac{4}{3}$π+4-4$\sqrt{3}$.
如图,将矩形ABCD绕对角线的交点0逆时针旋转90°得到矩形EFGH,已知AB=2,BC=2$\sqrt{3}$,则由旋转得到的阴影部分的面积为$\frac{4}{3}$π+4-4$\sqrt{3}$.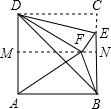 将-张正方形纸片ABCD对折,使CD与AB重合,得到折痕MN后展开,E为CN上-点,将△CDE沿DE所在的直线折叠,使得点C落在折痕MN上的点F处,连接AF,BF,BD,则得下列结论:
将-张正方形纸片ABCD对折,使CD与AB重合,得到折痕MN后展开,E为CN上-点,将△CDE沿DE所在的直线折叠,使得点C落在折痕MN上的点F处,连接AF,BF,BD,则得下列结论: