题目内容
20．关于x的一元二次方程ax2-2x+1=0有实数根，则a的取值范围是a≤1且a≠0．分析 根据一元二次方程的定义和根的判别式的意义得到a≠0且△=（-2）2-4a≥0，然后求出a的取值范围．
解答 解：∵一元二次方程ax2-2x+1=0有实数根，
∴△=（-2）2-4a≥0，且a≠0，
解得：a≤1且a≠0，
故答案为：a≤1且a≠0．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．也考查了一元二次方程的定义．
练习册系列答案
相关题目
11．
如图，将正六边形ABCDEF放置在直角坐标系内，A（-2，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2016次翻转之后，点C的坐标是（ ）
如图，将正六边形ABCDEF放置在直角坐标系内，A（-2，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2016次翻转之后，点C的坐标是（ ）| A． | （4032，0） | B． | （4032，2$\sqrt{3}$） | C． | （4031，$\sqrt{3}$） | D． | （4033，$\sqrt{3}$） |
8．若点A（m，y1），B（m+1，y2）都在二次函数y=ax2+4ax+2（a＞0）的图象上，且y1＜y2，则m的取值范围是（ ）
| A． | m＞-$\frac{5}{2}$ | B． | m≥-2 | C． | m＜-1 | D． | m≤-3 |
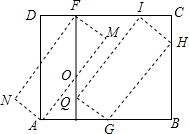如图所示，将矩形ABCD纸板剪出一个宽AE=5的矩形AEFD，再将它绕着中心O顺时针旋转，使其中两个顶点分别与点A和点F重合，得到矩形AMFN，再沿着直线AB向右平移使点M和点N分别落在边BC和边EF上，得到矩形GHIJ，当$\frac{AD}{AB}$=$\frac{5}{6}$时，矩形ABCD的周长为66．
12．
如图，在空白网格内将某一个小正方形涂成阴影部分，且所涂的小正方形与原阴影图形的小正方形至少有一边重合．小红按要求涂了一个正方形，所得到的阴影图形恰好是轴对称图形的概率为（ ）
如图，在空白网格内将某一个小正方形涂成阴影部分，且所涂的小正方形与原阴影图形的小正方形至少有一边重合．小红按要求涂了一个正方形，所得到的阴影图形恰好是轴对称图形的概率为（ ）| A． | $\frac{1}{5}$ | B． | $\frac{4}{15}$ | C． | $\frac{4}{9}$ | D． | $\frac{1}{3}$ |
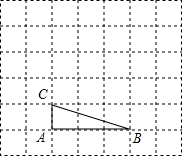如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．