题目内容
16. 完成下列证明过程,求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
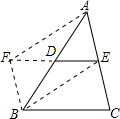
完成下列证明过程,求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.已知:在△ABC中,AD=DB,AE=EC
求证:DE∥BC,DE=$\frac{1}{2}$BC.
证明:延长ED到点F,使DF=DE,连接FA、FB、BE.
分析 根据文字题目证明要求写出已知、求证即可.先证明四边形AEBF是平行四边形,再证明四边形BCEF是平行四边形即可.
解答 解:已知:在△ABC中,AD=DB,AE=EC,求证:DE∥BC,DE=$\frac{1}{2}$BC.
故答案为:在△ABC中,AD=DB,AE=EC;DE∥BC,DE=$\frac{1}{2}$BC.
证明:延长ED到点F,使DF=DE,连接FA、FB、BE.
∵AD=BD,DE=DF
∴四边形AEBF是平行四边形.
∴BF∥AE,BF=AE,DE=$\frac{1}{2}$EF,
∵AE=EC,∴BF∥CE,BF=CE,
∴四边形BCEF是平行四边形.
∴DE∥BC,EF=BC,
∴DE=$\frac{1}{2}$EF=$\frac{1}{2}$BC.
点评 本题考查三角形中位线定理、平行四边形的判定和性质等知识,解题的关键是出现中点想到三角形中位线定理,记住三角形中位线平行于第三边且等于第三边的一半,属于中考常考题型.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
18.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
| A. | 7 | B. | 10 | C. | 35 | D. | 70 |
11. 如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )
如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )
 如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )
如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )| A. | (4032,0) | B. | (4032,2$\sqrt{3}$) | C. | (4031,$\sqrt{3}$) | D. | (4033,$\sqrt{3}$) |
8.若点A(m,y1),B(m+1,y2)都在二次函数y=ax2+4ax+2(a>0)的图象上,且y1<y2,则m的取值范围是( )
| A. | m>-$\frac{5}{2}$ | B. | m≥-2 | C. | m<-1 | D. | m≤-3 |
6.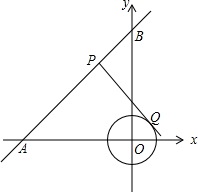 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{119}}{5}$ | C. | 2.4 | D. | 3 |
 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若EF=2,BC=10,则AB的长为6.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若EF=2,BC=10,则AB的长为6.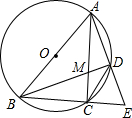 如图,△ABC内接于⊙O,AB是⊙O的直径,点D是劣弧AC上的一点,连结AD并延长与BC的延长线交于点E,AC、BD相交于点M.
如图,△ABC内接于⊙O,AB是⊙O的直径,点D是劣弧AC上的一点,连结AD并延长与BC的延长线交于点E,AC、BD相交于点M.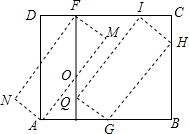 如图所示,将矩形ABCD纸板剪出一个宽AE=5的矩形AEFD,再将它绕着中心O顺时针旋转,使其中两个顶点分别与点A和点F重合,得到矩形AMFN,再沿着直线AB向右平移使点M和点N分别落在边BC和边EF上,得到矩形GHIJ,当$\frac{AD}{AB}$=$\frac{5}{6}$时,矩形ABCD的周长为66.
如图所示,将矩形ABCD纸板剪出一个宽AE=5的矩形AEFD,再将它绕着中心O顺时针旋转,使其中两个顶点分别与点A和点F重合,得到矩形AMFN,再沿着直线AB向右平移使点M和点N分别落在边BC和边EF上,得到矩形GHIJ,当$\frac{AD}{AB}$=$\frac{5}{6}$时,矩形ABCD的周长为66.