题目内容
7.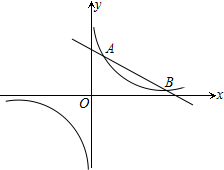 如图,双曲线$y=\frac{k}{x}$(k>0)与直线$y=-\frac{1}{2}x+4$相交于A、B两点
如图,双曲线$y=\frac{k}{x}$(k>0)与直线$y=-\frac{1}{2}x+4$相交于A、B两点(1)当k=6时,求点A、B的坐标
(2)在双曲线$y=\frac{k}{x}$(k>0)的同一支上有三点M(x1,y1),N(x2,y2),P($\frac{{{y_1}+{y_2}}}{2}$,y0),请你借助图象,直接写出y0与$\frac{{{y_1}+{y_2}}}{2}$的大小关系.
分析 (1)将x=6代入双曲线解析式中,将直线解析式代入双曲线解析式中得到关于x的一元二次方程,解方程即可求出A、B两点的横坐标,将其代入直线解析式中即可得出结论;
(2)根据函数图象,找出线段MN除两端点外的部分与反比例函数图象的上下位置关系,即可得出结论.
解答 解:(1)当k=6时,令$\frac{6}{x}$=-$\frac{1}{2}$x+4,
整理得:x2-8x+12=0,
解得:x=2或x=6.
∴点A的坐标为(2,3),点B的坐标为(6,1).
(2)当三点在第一象限时,线段MN除两端点外的部分在反比例函数图象的上方,
∴$\frac{{{y_1}+{y_2}}}{2}$>y0;
当三点在第三象限时,线段MN除两端点外的部分在反比例函数图象的下方,
∴$\frac{{{y_1}+{y_2}}}{2}$<y0.
点评 本题考查了反比例函数与一次函数交点的问题以及解一元二次方程,解题的关键是:(1)将直线解析式代入双曲线解析式中求出A、B点的横坐标;(2)利用函数图象的上下位置关系得出结论.本题属于基础题,难度不大,解决该题型题目时,联立两函数解析式成方程组,解方程组即可求出交点坐标.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
18.下列计算正确的是( )
| A. | x3÷x=x3 | B. | x3•x2=x5 | C. | (x3)2=x5 | D. | (2x)3=6x3 |
19.若一元二次方程-3x2+6x+m=0有实根,则m的取值范围是( )
| A. | m≤-3 | B. | m<-3 | C. | m≥-3 | D. | m>-3 |
16.使分式$\frac{1}{x-1}$有意义的x的取值范围是( )
| A. | x≠1 | B. | x≠-1 | C. | x<1 | D. | x>1 |
19.化简$\frac{16-{a}^{2}}{{a}^{2}+4a+4}$÷$\frac{a-4}{2a+4}$•$\frac{a-2}{a+4}$,其结果是( )
| A. | -2 | B. | 2 | C. | -$\frac{2(a-2)}{a+2}$ | D. | $\frac{2}{(a+2)^{2}}$ |
16. 如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )
如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )
 如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )
如图,l1∥l2∥l3,BC=1,$\frac{DF}{EF}$=3,则AB长为( )| A. | 4 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |