题目内容
19．若一元二次方程-3x2+6x+m=0有实根，则m的取值范围是（ ）| A． | m≤-3 | B． | m＜-3 | C． | m≥-3 | D． | m＞-3 |
分析 由方程有实数根结合根的判别式可得出关于m的一元一次不等式，解不等式即可得出结论．
解答 解：∵方程-3x2+6x+m=0有实根，
∴△=62-4×（-3）m≥0，
解得：m≥-3．
故选C．
点评 本题考查了根的判别式以及解一元一次不等式，解题的关键是根据根的情况得出关于m的一元一次不等式．本题属于基础题，难度不大，解决该题型题目时，根据根的个数结合根的判别式得出方程（或不等式）是关键．
练习册系列答案
相关题目
10．已知关于x的一元二次方程x2+3x+k=0有实数根，则下列四个数中，满足条件的k值为（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
4．
了了解九年级男生的立定跳远成绩，体育老师对该校九年级的260位男生进行了一次立定跳远测试．已知，九年级男生立定跳远成绩（x）的达标要求是：x＜185为不合格；185≤x＜225为合格；x≥225为优秀（单位：cm）．随机以40位男为生的测试数据为样本，绘制出部分频数分布表和部分频数分布直方图，如下所示：
请结合图表完成下列问题：
（1）请把频数分布表和频数分布直方图补充完整；
（2）这个样本数据的中位数落在第几组？
（3）估计该校九年级男生立定跳远成绩为优秀的有多少人？
了了解九年级男生的立定跳远成绩，体育老师对该校九年级的260位男生进行了一次立定跳远测试．已知，九年级男生立定跳远成绩（x）的达标要求是：x＜185为不合格；185≤x＜225为合格；x≥225为优秀（单位：cm）．随机以40位男为生的测试数据为样本，绘制出部分频数分布表和部分频数分布直方图，如下所示：| 组别 | 成绩x（cm） | 频数（人数） |
| 第1组 | 165≤x＜185 | 4 |
| 第2组 | 185≤x＜205 | 6 |
| 第3组 | 205≤x＜225 | |
| 第4组 | 225≤x＜245 | 18 |
| 第5组 | 245≤x＜265 | 4 |
（1）请把频数分布表和频数分布直方图补充完整；
（2）这个样本数据的中位数落在第几组？
（3）估计该校九年级男生立定跳远成绩为优秀的有多少人？
11．A，B两种机器人都被用来搬运化工原料，A型机器人比B型机器人每小时多搬运40千克，A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等．设B型机器人每小时搬运化工原料x千克，根据题意可列方程为（ ）
| A． | $\frac{1200}{x+40}$=$\frac{800}{x}$ | B． | $\frac{1200}{x-40}$=$\frac{800}{x}$ | C． | $\frac{1200}{x}$=$\frac{800}{x-40}$ | D． | $\frac{1200}{x}$=$\frac{800}{x+40}$ |
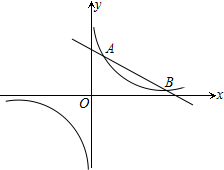如图，双曲线$y=\frac{k}{x}$（k＞0）与直线$y=-\frac{1}{2}x+4$相交于A、B两点
8．
如图，在边长为4的菱形ABCD中，∠BAD=120°，则对角线AC的长为（ ）
如图，在边长为4的菱形ABCD中，∠BAD=120°，则对角线AC的长为（ ）| A． | 4 | B． | 2 | C． | 2$\sqrt{3}$ | D． | 3 |