Question

16．已知三角形ABC在平面直角坐标系中，点A（3，6），点B（1，3），点C（4，2），则三角形ABC的面积为多少？

Answer 1

分析 根据坐标画出图形，利用割补法计算三角形的面积即可求解．

解答 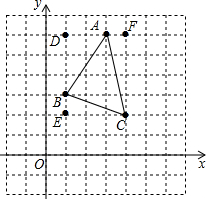解：D的坐标是（，1，6），E的坐标是（1，2），F的坐标是（4，6）．
则AD=2，BD=3，则S_△ABD=$\frac{1}{2}$AD•BD=$\frac{1}{2}$×2×3=3，
AF=1，CF=4，则S_△ACF=$\frac{1}{2}$AF•CF=$\frac{1}{2}$×1×4=2；
BE=1，EC=3，则S_△BEC=$\frac{1}{2}$BE•EC=$\frac{1}{2}$×1×3=$\frac{3}{2}$；
S_{四边形DECF}=EC•CF=3×4=12，
则S_△ABC=S_{四边形DECF}-S_△ABD-S_△ACF-S_△BEC=12-3-2-$\frac{3}{2}$=$\frac{11}{2}$．

点评 本题考查了坐标与图形性质：利用点的坐标特征计算相应的线段长和判断线段与坐标轴的位置关系；记住各象限内点的坐标特征和坐标上点的坐标特征．