题目内容
17.计算:(1)(-$\sqrt{5}$)2+3$\sqrt{3}$×$\sqrt{12}$.
(2)$\sqrt{(1-\sqrt{3})^{2}}$-($\sqrt{3}$)2×$\sqrt{6}$÷$\sqrt{2}$.
(3)(8×27)${\;}^{\frac{1}{3}}$-(π-1)0-($\frac{1}{2}$)-1;
(4)$\sqrt{2}$×$\root{3}{18}$×$\root{6}{6}$.
分析 (1)先计算平方,再相乘;
(2)先开方,因为1-$\sqrt{3}$<0,所以$\sqrt{(1-\sqrt{3})^{2}}$=$\sqrt{3}$-1,再乘除;
(3)8×27的立方根据为2×3=6,零次幂为1;
(4)都化成2和3的分数指数幂,再根据同底数幂相乘.
解答 解:(1)(-$\sqrt{5}$)2+3$\sqrt{3}$×$\sqrt{12}$,
=5+3$\sqrt{36}$,
=5+18,
=23,
(2)$\sqrt{(1-\sqrt{3})^{2}}$-($\sqrt{3}$)2×$\sqrt{6}$÷$\sqrt{2}$,
=$\sqrt{3}$-1-3$\sqrt{6}$÷$\sqrt{2}$,
=$\sqrt{3}$-1-3$\sqrt{3}$,
=-2$\sqrt{3}$-1,
(3)(8×27)${\;}^{\frac{1}{3}}$-(π-1)0-($\frac{1}{2}$)-1,
=2×3-1-2,
=6-3,
=3,
(4)$\sqrt{2}$×$\root{3}{18}$×$\root{6}{6}$,
=${2}^{\frac{1}{2}}$×${2}^{\frac{1}{3}}$×${3}^{\frac{2}{3}}$×${2}^{\frac{1}{6}}$×${3}^{\frac{1}{6}}$,
=${2}^{\frac{1}{2}+\frac{1}{3}+\frac{1}{6}}$×${3}^{\frac{2}{3}+\frac{1}{6}}$,
=2×${3}^{\frac{5}{6}}$,
=2$\root{6}{243}$.
点评 本题是分数指数、负整数指数和零指数幂的计算,熟练掌握公式是关键:①零次幂:a0=1(a≠0);②负整数指数幂:a-p=$\frac{1}{{a}^{p}}$=$(\frac{1}{a})^{p}$;一般应用第二种方法进行计算,尤其是底数为分数的运算;③运算顺序:先计算括号里的,再计算乘方和开方,再乘除,最后算加减.

 阅读快车系列答案
阅读快车系列答案| A. | 直线x=0 | B. | 直线x=1 | C. | 直线x=-2 | D. | 直线x=-1 |
| 股票名称 | 每股净赚(元) | 股数 |
| 长城 | +23 | 500 |
| 北斗 | -3 | 1000 |
| 白马 | +1.5 | 1000 |
| 海潮 | -7 | 500 |
 已知:两条定直线a,b在直线a上有一个定点A,在直线a上求一点B,在直线b上求一点P,使两点A、B与点P的连线总长最短.
已知:两条定直线a,b在直线a上有一个定点A,在直线a上求一点B,在直线b上求一点P,使两点A、B与点P的连线总长最短.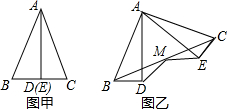 已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME.
已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME. 如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值.
如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值.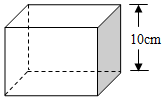 如图,某玩具厂要制作一批体积为1000cm3的长方体包装盒,其高为10cm.按设计需要,底面应做成正方形.求底面边长应是多少?
如图,某玩具厂要制作一批体积为1000cm3的长方体包装盒,其高为10cm.按设计需要,底面应做成正方形.求底面边长应是多少?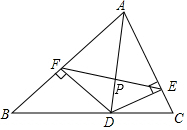 如图,AD是△ABC的角平分线,DF⊥AB于F,DE⊥AC于E,连EF,交AD于点P.
如图,AD是△ABC的角平分线,DF⊥AB于F,DE⊥AC于E,连EF,交AD于点P.