题目内容
2.抛物线y=ax2+bx+c(a≠0)过(2,8)和(-6,8)两点,则此抛物线的对称轴为( )| A. | 直线x=0 | B. | 直线x=1 | C. | 直线x=-2 | D. | 直线x=-1 |
分析 由二次函数的对称性可求得抛物线的对称轴
解答 解:
∵抛物线y=ax2+bx+c(a≠0)过(2,8)和(-6,8)两点,
∴抛物线的对称轴为x=$\frac{2+(-6)}{2}$=-2,
故选C.
点评 本题主要考查二次函数的性质,掌握二次函数图象上关于对称轴对称的点所对应的函数值相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.一个多边形的内角和是1260°,这个多边形的边数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
7.用火柴棒按如图中的方式搭图形,则搭第7个图形所需火柴棒的根数为( )


| A. | 28 | B. | 29 | C. | 34 | D. | 35 |
 用一个圆心角为120°、半径为18cm的扇形作一个圆锥的侧面.求圆锥底面积圆的半径R.
用一个圆心角为120°、半径为18cm的扇形作一个圆锥的侧面.求圆锥底面积圆的半径R.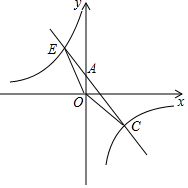 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax﹢b的图象交于C(4,-3),E(-3,4)两点.且一次函数图象交y轴于点A.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax﹢b的图象交于C(4,-3),E(-3,4)两点.且一次函数图象交y轴于点A. 张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案:
张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案: