题目内容
2. 如图,已知等边△ABC.
如图,已知等边△ABC.(1)用直尺和圆规作出△ABC的外接圆;
(2)若AB=4$\sqrt{3}$,求△ABC的外接圆半径R.
分析 (1)分别作出AC和BC的垂直平分线,两线的交点就是圆心O的位置,再以CO长为半径画圆即可;
(2)当△ABC是正三角形时,BC的垂直平分线过A点,首先根据等腰三角形三线合一的性质计算出∠OCF=30°,再根据勾股定理计算出CO的长度即可.
解答 解:(1)如图所示:⊙O即为所求;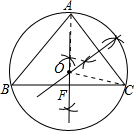
(2)当△ABC是正三角形时,BC的垂直平分线过A点,
连接AO,CO,
∵△ABC是正三角形,AF⊥BC,
∴∠FAC=$\frac{1}{2}$∠BAC=30°,CF=$\frac{1}{2}$BC=2$\sqrt{3}$,
∵AO=CO,
∴∠ACO=30°,
∴∠OCF=60°-30°=30°,
∴OF=$\frac{1}{2}$OC,
设OC=2x,则OF=x,
x2+(2$\sqrt{3}$)2=(2x)2,
解得:x=2或x=-2(舍),
∴R=2OF=4.
点评 此题主要考查了三角形外接圆以及利用勾股定理,基本作图,关键是掌握如何确定三角形外接圆的圆心:其中两条边的垂直平分线的交点.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
12.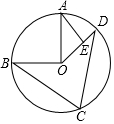 如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )
如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )
 如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )
如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
13.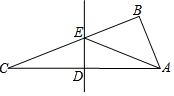 如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
 如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
10.下列计算正确的是( )
| A. | (-x2)3=-x6 | B. | x4•x2=x8 | C. | (x3)2=-x5 | D. | x3•x2=2x6 |
14.已知a,b互为相反数,c,d互为倒数,x的绝对值是2,计算x2-cd•x+(a+b)2017=( )
| A. | 2或-2 | B. | 2或6 | C. | 2 | D. | 3 |
12.某水果公司把一批水果运到外地,现有汽车和火车两种运输方式可供选择,运输过程中的损耗均为100元/时.其它主要参考数据如下:
(1)请分别写出汽车、火车运输的总费用y(元)与运输路程x(千米)之间的关系式;(提示:总费用=运输费+损耗费+袋卸费)
(2)当运输路程x(千米)为多少时,汽车、火车两种运输方式的总费用相同.
| 运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费(元) |
| 汽车 | 50 | 20 | 900 |
| 火车 | 100 | 15 | 2000 |
(2)当运输路程x(千米)为多少时,汽车、火车两种运输方式的总费用相同.
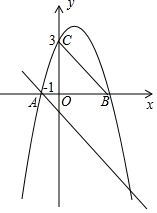 如图,二次函数y=ax2+2x+c的图象与x轴交于点A(-1,0)和点B,与y轴交于点C(0,3),过点A的直线AD∥BC,交抛物线于另一点D.
如图,二次函数y=ax2+2x+c的图象与x轴交于点A(-1,0)和点B,与y轴交于点C(0,3),过点A的直线AD∥BC,交抛物线于另一点D.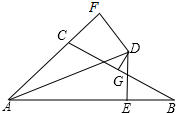 如图∠BAC的平分线AD与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=22,AC=10,则BE=6.
如图∠BAC的平分线AD与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=22,AC=10,则BE=6.