题目内容
1. 如图,P为⊙O直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π.
如图,P为⊙O直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π.
分析 连接OC、OD,利用同底等高的三角形面积相等可知阴影部分的面积等于扇形OCD的面积,然后计算扇形面积就可.
解答 解:连接OC、OD、CD.
∵△COD和△CPD等底等高,
∴S△COD=S△PCD.
∵点C,D为半圆的三等分点,
∴∠COD=180°÷3=60°,
∴阴影部分的面积=S扇形COD=$\frac{60π×{6}^{2}}{360}$=6π.
故答案为:6π.
点评 此题主要考查了扇形面积求法,利用已知得出理解阴影部分的面积等于扇形OCD的面积是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.在平面直角坐标系中,点P(-3,2)关于直线y=x对称点的坐标是( )
| A. | (-3,-2) | B. | (3,2) | C. | (2,-3) | D. | (3,-2) |
13.已知点C是线段AB的黄金分割点(AC>BC),AC=4,则线段AB的长为( )
| A. | 2$\sqrt{5}$-2 | B. | 2$\sqrt{5}$+2 | C. | 6-2$\sqrt{5}$ | D. | 6+2$\sqrt{5}$ |
10.某剧院的观众席的座位为扇形,且按下列方式设置:
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
| 排数(x) | 1 | 2 | 3 | 4 | … |
| 座位数(y) | 50 | 53 | 56 | 59 | … |
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
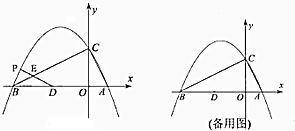
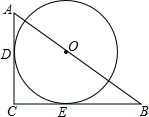 如图,⊙O与Rt△ACB的两直角边AC、BC相切,切点分别为D、E两点,且圆心O在斜边AB上.
如图,⊙O与Rt△ACB的两直角边AC、BC相切,切点分别为D、E两点,且圆心O在斜边AB上. 如图,已知一次函数y=kx+b的图象与x轴交于点(3,0),与y轴交于点(0,2),不等式kx+b≥2解集是x≤0.
如图,已知一次函数y=kx+b的图象与x轴交于点(3,0),与y轴交于点(0,2),不等式kx+b≥2解集是x≤0.