题目内容
11.如图,在△ABC中,点A,B分别在x轴的正、负半轴上(其中OA<OB),点C在y轴的正半轴上,AB=10,OC=4,∠ABC=∠ACO.(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点D的坐标为(-4,0),P是该抛物线上的一个动点.
①直线DP交直线BC于点E,当△BDE是等腰三角形时,直接写出此时点E的坐标;
②连结CD,CP,若∠PCD=∠CBD,请求出点P的坐标.
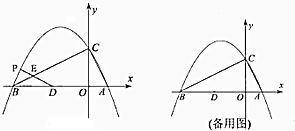
分析 
(1)利用△BOC~△C0A得出比例式求出OA,OB,从而得出A(2,0),B(-8,0),再利用两根式求解析式的方法即可求解;
(2)①根据点E在直线BC上,设出点E的坐标,再根据平面坐标系中两点间的距离公式分别求出BE=$\sqrt{{(m+8}^{)2}{+(\frac{1}{2}m+4)}^{2}}$,DE=$\sqrt{{(m+4)}^{2}{+(\frac{1}{2}m+4)}^{2}}$,BD=4,而△BDE为等腰三角形,分三种情况:BE=BD,BE=DE,BD=DE,再求解方程,从而得到点E的坐标;
②根据∠PCD=∠CBD作出直角三角形,利用平面坐标系中互相垂直的直线的比例系数之积为-1,根据直线CD的解析式为y=x+4,设出直线PF的解析式为y=-x+4,利用锐角的三角函数求出CF=2PF,设出点P的坐标,确定出CF=$\frac{|{\frac{1}{4}m}^{2}+\frac{1}{2}m|}{2}$,PF=$\frac{|{\frac{1}{4}m}^{2}+\frac{5}{2}m|}{2}$,求解绝对值方程即可.
解答 解:(1)设OA=x,则OB=10-x,
∴∠ABC=∠ACO,∠AOC=∠COB,
∴△BOC~△C0A,
∴$\frac{OB}{OC}$=$\frac{OC}{OA}$,
∴OC2=OA×OB,
∴16=x(10-x),
∴x=8或x=2,
∴A(2,0),B(-8,0),
设抛物线的解析式为y=a(x+8)(x-2)
∴4=(0+8)(0-2),
∴a=-$\frac{1}{4}$,
∴y=-$\frac{1}{4}$(x+8)(x-2)=-$\frac{1}{4}$x2-$\frac{3}{2}$x+4.
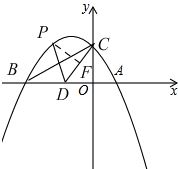
(2)
①∵B(-8,0),C(0,4),
∴直线BC的解析式为y=$\frac{1}{2}$x+4,
设E(m,m+4),且B(-8,0),D(0,4),
∴BE=$\sqrt{{(m+8}^{)2}{+(\frac{1}{2}m+4)}^{2}}$,DE=$\sqrt{{(m+4)}^{2}{+(\frac{1}{2}m+4)}^{2}}$,BD=4,
∵△BDE为等腰三角形,
Ⅰ、当BE=DE时,有$\sqrt{{(m+8}^{)2}{+(\frac{1}{2}m+4)}^{2}}$=$\sqrt{{(m+4)}^{2}{+(\frac{1}{2}m+4)}^{2}}$,
∴m=-6,
∴$\frac{1}{2}$m+4=1,
∴E(-6,1),
Ⅱ、当BE=BD时,有$\sqrt{{(m+8}^{)2}{+(\frac{1}{2}m+4)}^{2}}$=4,
∴m=$\frac{-40+8\sqrt{5}}{5}$或m=$\frac{-40-8\sqrt{5}}{5}$,
∴E($\frac{-40+8\sqrt{5}}{5}$,$\frac{4\sqrt{5}}{5}$),E($\frac{-40-8\sqrt{5}}{5}$,-$\frac{4\sqrt{5}}{5}$),
Ⅲ、当BD=DE时,有$\sqrt{{(m+4)}^{2}{+(\frac{1}{2}m+4)}^{2}}$=4,
∴m=-$\frac{8}{5}$或m=-8(舍)
∴E(-$\frac{8}{5}$,$\frac{16}{5}$),
∴E(-6,1),E($\frac{-40+8\sqrt{5}}{5}$,$\frac{4\sqrt{5}}{5}$),E($\frac{-40-8\sqrt{5}}{5}$,-$\frac{4\sqrt{5}}{5}$),E(-$\frac{8}{5}$,$\frac{16}{5}$).
②∵C(0,4),D(-4,0),
∴直线CD的解析式为y=x+4,
作PF⊥CD,设直线PF的解析式为y=-x+b,
∴F($\frac{b-4}{2}$,$\frac{b+4}{2}$),
设P(m,-m+b),
∴-m+b=-$\frac{1}{4}$m2-$\frac{3}{2}$m+4,
∴b=-$\frac{1}{4}$m2-$\frac{1}{2}$m+4,
∵P(-m,-m+b),F($\frac{b-4}{2}$,$\frac{b+4}{2}$),C(0,4),
∴CF=$\sqrt{{(\frac{b-4}{2})}^{2}+{(\frac{b+4}{2})}^{2}}$=$\frac{|{\frac{1}{4}m}^{2}+\frac{1}{2}m|}{2}$,
PF=$\sqrt{{(m-\frac{b-4}{2})}^{2}{+(-m+b+\frac{b+4}{2})}^{2}}$=$\frac{|{\frac{1}{4}m}^{2}+\frac{5}{2}m|}{2}$,
∵tan∠CBD=$\frac{1}{2}$,∠CBD=∠PCF,
∴tan∠PCF=$\frac{PF}{CF}$=$\frac{1}{2}$,
∴CF=2PF,
∴$\frac{|{\frac{1}{4}m}^{2}+\frac{1}{2}m|}{2}$=2×$\frac{|{\frac{1}{4}m}^{2}+\frac{5}{2}m|}{2}$,
∴m=-$\frac{22}{3}$或m=-18,
∴b=-$\frac{1}{4}$m2-$\frac{1}{2}$m+4=-$\frac{52}{9}$或b=-$\frac{1}{4}$m2-$\frac{1}{2}$m+4=-68,
∴P(-$\frac{22}{3}$,$\frac{14}{9}$)或P(-18,-50).
点评 本题是二次函数的综合题,涉及到的知识点有,平面坐标系中两点间的距离公式,如BE=$\sqrt{{(m+8}^{)2}{+(\frac{1}{2}m+4)}^{2}}$,DE=$\sqrt{{(m+4)}^{2}{+(\frac{1}{2}m+4)}^{2}}$,BD=4,相似矩形的判定和性质,求解方程,解题的关键是利用平面坐标系中两点间的距离公式和作出辅助线.

 某同学在距电视塔BC塔底水平距离200米的A处,看塔顶C的仰角为20°(不考虑身高因素),则此塔BC的高约为( )
某同学在距电视塔BC塔底水平距离200米的A处,看塔顶C的仰角为20°(不考虑身高因素),则此塔BC的高约为( )(参考数据:sin20°≈0.3420,cos20°≈0.9397,tan20°≈0.3640)(保留到个位)
| A. | 68米 | B. | 73米 | C. | 127米 | D. | 188米 |
| A. | $\sqrt{3}$ | B. | $±\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $±\frac{\sqrt{3}}{3}$ |
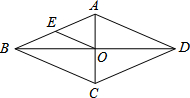 在菱形ABCD中,E为AB的中点,OE=3,则菱形ABCD的周长为24.
在菱形ABCD中,E为AB的中点,OE=3,则菱形ABCD的周长为24. 如图,要使宽为2米的矩形平板车ABCD通过宽为2$\sqrt{2}$米的等宽的直角通道,平板车的长不能超过4米.
如图,要使宽为2米的矩形平板车ABCD通过宽为2$\sqrt{2}$米的等宽的直角通道,平板车的长不能超过4米.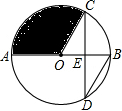 如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分面积为( )
如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分面积为( ) 如图,P为⊙O直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π.
如图,P为⊙O直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π.