题目内容
12.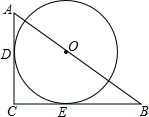 如图,⊙O与Rt△ACB的两直角边AC、BC相切,切点分别为D、E两点,且圆心O在斜边AB上.
如图,⊙O与Rt△ACB的两直角边AC、BC相切,切点分别为D、E两点,且圆心O在斜边AB上.(1)试判断以O、D、C、E为顶点的四边形是什么特殊的四边形,并说明理由.
(2)若AC=6,BC=8,求⊙O的半径长.
分析 (1)首先连接OD,OE,由⊙O与Rt△ACB的两直角边AC、BC相切,可得以O、D、C、E为顶点的四边形是矩形,又由OD=OE,即可得四边形ODCE是正方形;
(2)首先设OD=x,由四边形ODCE是正方形,可证得△AOD∽△ABC,然后由相似三角形的对应边成比例,求得答案.
解答 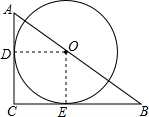 解:(1)以O、D、C、E为顶点的四边形是正方形.
解:(1)以O、D、C、E为顶点的四边形是正方形.
理由:连接OD,OE,
∵⊙O与Rt△ACB的两直角边AC、BC相切,
∴OD⊥AC,OE⊥BC,
∴∠ODC=∠OEC=90°,
∵∠C=90°,
∴四边形ODCE是矩形,
∵OD=OE,
∴四边形ODCE是正方形;
(2)设OD=x,
∵四边形ODCE是正方形,
∴CD=OD=x,OD∥BC,
则AD=AC-CD=6-x,
∴△AOD∽△ABC,
∴$\frac{OD}{BC}$=$\frac{AD}{AC}$,
即$\frac{x}{8}=\frac{6-x}{6}$,
解得:x=$\frac{24}{7}$,
∴⊙O的半径长为:$\frac{24}{7}$.
点评 此题考查了切线的性质、矩形的性质、正方形的判定与性质以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
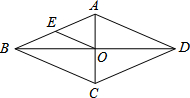 在菱形ABCD中,E为AB的中点,OE=3,则菱形ABCD的周长为24.
在菱形ABCD中,E为AB的中点,OE=3,则菱形ABCD的周长为24.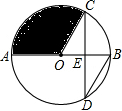 如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分面积为( )
如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分面积为( )
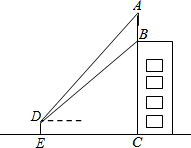 如图,某建筑物BC顶部接收塔AB,且点A,B,C在同一条直线上,小明在D处观接收塔顶部A的仰角为45°,观测旗杆底部B的仰角为30°.已知点D到地面的距离DE为1.7m,EC=30m,求接收塔AB的高度和建筑物BC的高度(结果保留根号).
如图,某建筑物BC顶部接收塔AB,且点A,B,C在同一条直线上,小明在D处观接收塔顶部A的仰角为45°,观测旗杆底部B的仰角为30°.已知点D到地面的距离DE为1.7m,EC=30m,求接收塔AB的高度和建筑物BC的高度(结果保留根号). 用圆规、直尺作图,不写作法,但要保留作图痕迹.
用圆规、直尺作图,不写作法,但要保留作图痕迹. 如图,P为⊙O直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π.
如图,P为⊙O直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π.