题目内容
11．化简：（$\frac{{m}^{2}}{m-1}+\frac{1}{1-m}$）÷（m2+2m+1）分析 原式括号中第二项变形后，利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果．
解答 解：原式=$\frac{{m}^{2}-1}{m-1}$•$\frac{1}{（m+1）^{2}}$=$\frac{（m+1）（m-1）}{m-1}$•$\frac{1}{（m+1）^{2}}$=$\frac{1}{m+1}$．
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
智能训练练测考系列答案
相关题目
如图，P为⊙O直径AB上的一个动点，点C，D为半圆的三等分点，若AB=12，则图中阴影部分的面积为6π．
6．如图，若将如图正方形剪成四块，恰好能拼成如图的矩形，则$\frac{a}{b}$等于（ ）
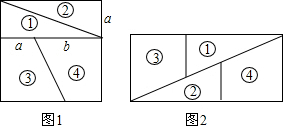
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{5}+1}{2}$ | D． | $\frac{\sqrt{5}-1}{2}$ |
