题目内容
 如图,在平面直角坐标系中,已知点A(2,0),以OA为边在第一象限内作等边三角形OAB,点P是x轴上一动点 (点P在点A的右侧),以线段BP为边作等边三角形BPQ.设点Q的坐标为(x,y),则y与x之间的关系式是
如图,在平面直角坐标系中,已知点A(2,0),以OA为边在第一象限内作等边三角形OAB,点P是x轴上一动点 (点P在点A的右侧),以线段BP为边作等边三角形BPQ.设点Q的坐标为(x,y),则y与x之间的关系式是考点:等边三角形的性质,待定系数法求一次函数解析式
专题:
分析:分两种情况:
①当Q在x轴上方时,由△OAB和△BPQ都为等边三角形,等边三角形的边长相等,且每一个内角都为60°,得到∠OBA=∠QBP,等号两边都加上∠ABP,得到∠OBP=∠ABQ,根据“SAS”得到△OBP≌△ABQ,即可得到∠BAQ=∠BOP,从而求得∠QAP=60°,通过解直角三角形即可求得y与x之间的关系式;
②当Q在x轴下方时,由△OAB和△BPQ都为等边三角形,等边三角形的边长相等,且每一个内角都为60°,得到∠OBA=∠QBP,等号两边都减去∠ABP,得到∠BOQ=∠BAP,根据“SAS”得到△OBQ≌△ABP,即可得到∠BOQ=∠BAP,进而求得∠NOQ=60°,通过解直角三角形即可求得y与x之间的关系式.
①当Q在x轴上方时,由△OAB和△BPQ都为等边三角形,等边三角形的边长相等,且每一个内角都为60°,得到∠OBA=∠QBP,等号两边都加上∠ABP,得到∠OBP=∠ABQ,根据“SAS”得到△OBP≌△ABQ,即可得到∠BAQ=∠BOP,从而求得∠QAP=60°,通过解直角三角形即可求得y与x之间的关系式;
②当Q在x轴下方时,由△OAB和△BPQ都为等边三角形,等边三角形的边长相等,且每一个内角都为60°,得到∠OBA=∠QBP,等号两边都减去∠ABP,得到∠BOQ=∠BAP,根据“SAS”得到△OBQ≌△ABP,即可得到∠BOQ=∠BAP,进而求得∠NOQ=60°,通过解直角三角形即可求得y与x之间的关系式.
解答: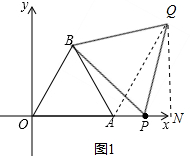 解:①当Q在x轴上方时,如图1,连接AQ,作QN⊥x轴于N,
解:①当Q在x轴上方时,如图1,连接AQ,作QN⊥x轴于N,
∵△OAB和△BPQ都为等边三角形,
∴OB=AB,BP=BQ,
∠OBA=∠QBP=60°,即∠OBA+∠ABP=∠QBP+∠ABP,
∴∠OBP=∠ABQ,
在△OBP和△ABQ中
∴△OBP≌△ABQ(SAS),
∴∠BAQ=∠BOP=60°,
又∵∠BAO=60°,
∴∠QAP=60°,
在直角三角形AQN中,tan60°=
,
∴
=
则y=QN=
(x-2),
∴y与x之间的关系式是:y=
x-2
;
②当Q在x轴下方时,如图2,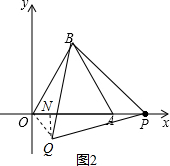 连接OQ,作QN⊥x轴于N,
连接OQ,作QN⊥x轴于N,
∵△OAB和△BPQ都为等边三角形,
∴OB=AB,BP=BQ,
∠OBA=∠QBP=60°,即∠OBA-∠ABP=∠QBP-∠ABP,
∴∠OBQ=∠ABP,
在△OBQ和△ABP中,
∴△OBQ≌△ABP(SAS),
∴∠BOQ=∠BAP,
∵∠BAP=∠AOB+∠ABO=120°,
∴∠BOQ=120°,
又∵∠BOA=60°,
∴∠NOQ=60°,
在直角三角形OQN中,tan60°=
,
∴
=
,
则y=-QN=-
x,
∴y与x之间的关系式是:y=-
x;
综上,y与x之间的关系式是y=
x-2
或y=-
x.
故答案为y=
x-2
或y=-
x.
 解:①当Q在x轴上方时,如图1,连接AQ,作QN⊥x轴于N,
解:①当Q在x轴上方时,如图1,连接AQ,作QN⊥x轴于N,∵△OAB和△BPQ都为等边三角形,
∴OB=AB,BP=BQ,
∠OBA=∠QBP=60°,即∠OBA+∠ABP=∠QBP+∠ABP,
∴∠OBP=∠ABQ,
在△OBP和△ABQ中
|
∴△OBP≌△ABQ(SAS),
∴∠BAQ=∠BOP=60°,
又∵∠BAO=60°,
∴∠QAP=60°,
在直角三角形AQN中,tan60°=
| QN |
| AN |
∴
| QN |
| x-2 |
| 3 |
则y=QN=
| 3 |
∴y与x之间的关系式是:y=
| 3 |
| 3 |
②当Q在x轴下方时,如图2,
 连接OQ,作QN⊥x轴于N,
连接OQ,作QN⊥x轴于N,∵△OAB和△BPQ都为等边三角形,
∴OB=AB,BP=BQ,
∠OBA=∠QBP=60°,即∠OBA-∠ABP=∠QBP-∠ABP,
∴∠OBQ=∠ABP,
在△OBQ和△ABP中,
|
∴△OBQ≌△ABP(SAS),
∴∠BOQ=∠BAP,
∵∠BAP=∠AOB+∠ABO=120°,
∴∠BOQ=120°,
又∵∠BOA=60°,
∴∠NOQ=60°,
在直角三角形OQN中,tan60°=
| QN |
| ON |
∴
| QN |
| x |
| 3 |
则y=-QN=-
| 3 |
∴y与x之间的关系式是:y=-
| 3 |
综上,y与x之间的关系式是y=
| 3 |
| 3 |
| 3 |
故答案为y=
| 3 |
| 3 |
| 3 |
点评:此题综合考查了等边三角形的性质,直角三角形的性质,三角形全等的判定与性质.求得三角形全等是本题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 在数学学习中,要经常证明一个命题是不是真命题,那么,我们证明了很多命题,请你回答下列问题.
在数学学习中,要经常证明一个命题是不是真命题,那么,我们证明了很多命题,请你回答下列问题. 如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1cm/秒的速度移动,点Q从点B开始沿BC边向点C以2cm/秒的速度移动.
如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1cm/秒的速度移动,点Q从点B开始沿BC边向点C以2cm/秒的速度移动.
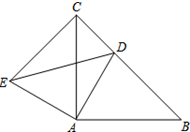 已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.
已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.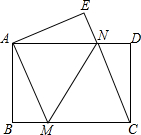 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.