题目内容
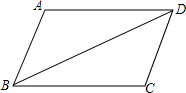 如图,已知:∠ABC=∠ADC,AD∥BC.请补充完整过程说明:AB=CD的理由.
如图,已知:∠ABC=∠ADC,AD∥BC.请补充完整过程说明:AB=CD的理由.证明:∵AD∥BC
∴
∵∠ABC=∠ADC (已知)
∴
在△ABD和△CDB中
∴△ABD≌△CDB(
∴AB=CD.
考点:全等三角形的判定与性质
专题:推理填空题
分析:根据AD∥BC,可得∠ADB=∠CBD,根据∠ABC=∠ADC可得∠ABD=∠CDB,即可证明△ABD≌△CDB,根据全等三角形对应边相等的性质可得即可解题.
解答:证明:∵AD∥BC
∴∠ADB=∠CBD(两直线平行,内错角相等 )
∵∠ABC=∠ADC ( 已 知 )
∴∠ABD=∠CDB( 等式的性质
在△ABD和△CDB中,
,
∴△ABD≌△CDB(ASA)
∴AB=CD.
故答案为:∠ADB、∠CBD、∠ABD、∠CDB、∠ADB、∠CBD、BD、BD、∠ABD、∠CDB、ASA.
∴∠ADB=∠CBD(两直线平行,内错角相等 )
∵∠ABC=∠ADC ( 已 知 )
∴∠ABD=∠CDB( 等式的性质
在△ABD和△CDB中,
|
∴△ABD≌△CDB(ASA)
∴AB=CD.
故答案为:∠ADB、∠CBD、∠ABD、∠CDB、∠ADB、∠CBD、BD、BD、∠ABD、∠CDB、ASA.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABD≌△CDB是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1cm/秒的速度移动,点Q从点B开始沿BC边向点C以2cm/秒的速度移动.
如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1cm/秒的速度移动,点Q从点B开始沿BC边向点C以2cm/秒的速度移动.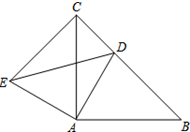 已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.
已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.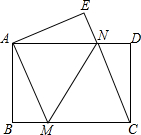 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N. 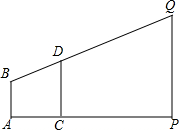 如图所示,旗杆顶部Q,标杆顶部D,观测者的眼睛B在同一直线上,测得观测者的脚到旗杆底部的距离AP=75m,观测者的脚到标杆底部的距离AC=2.5m,若AB=1.5m,标杆CD的高为2m,那么旗杆有多高.
如图所示,旗杆顶部Q,标杆顶部D,观测者的眼睛B在同一直线上,测得观测者的脚到旗杆底部的距离AP=75m,观测者的脚到标杆底部的距离AC=2.5m,若AB=1.5m,标杆CD的高为2m,那么旗杆有多高.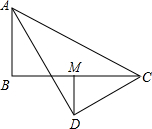 在Rt△ABC中,∠B=90°,AD平分∠BAC,CD⊥AD,垂足为D,DM⊥BC.
在Rt△ABC中,∠B=90°,AD平分∠BAC,CD⊥AD,垂足为D,DM⊥BC.