题目内容
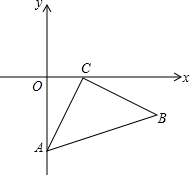 已知:在平面直角坐标系中,△ABC的顶点A(0,2),C(1,0)分别在y轴、x轴上,当点B在第四象限时,且∠ACB=90°,AC=BC.则点B的坐标为:(
已知:在平面直角坐标系中,△ABC的顶点A(0,2),C(1,0)分别在y轴、x轴上,当点B在第四象限时,且∠ACB=90°,AC=BC.则点B的坐标为:(证明:
考点:全等三角形的判定与性质,坐标与图形性质,等腰直角三角形
专题:
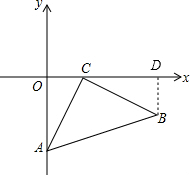
分析:作BD⊥x轴于D点,易证∠OAC=∠BCD,即可证明△OAC≌△DCB,可得CD=OA,BD=OC,即可解题.
解答:解:作BD⊥x轴于D点,
∵∠ACB=90°,
∴∠ACO+∠BCD=90°,
∵∠ACO+∠OAC=90°,
∴∠OAC=∠BCD,
在△OAC和△DCB中,
,
∴△OAC≌△DCB(AAS),
∴CD=OA=2,BD=OC=1,
∴OD=3,
∴点B坐标(3,-1).
故答案为:3,-1.

∵∠ACB=90°,
∴∠ACO+∠BCD=90°,
∵∠ACO+∠OAC=90°,
∴∠OAC=∠BCD,
在△OAC和△DCB中,
|
∴△OAC≌△DCB(AAS),
∴CD=OA=2,BD=OC=1,
∴OD=3,
∴点B坐标(3,-1).
故答案为:3,-1.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△OAC≌△DCB是解题的关键.

练习册系列答案
相关题目
 如图所示,它是由6个面积为1的正方形组成的矩形,点A、B、C、D、E、F、G是小正方形的顶点,以这七个点中的任意三个为顶点,可组成面积为1的三角形的个数是( )
如图所示,它是由6个面积为1的正方形组成的矩形,点A、B、C、D、E、F、G是小正方形的顶点,以这七个点中的任意三个为顶点,可组成面积为1的三角形的个数是( )| A、11个 | B、12个 |
| C、13个 | D、14个 |

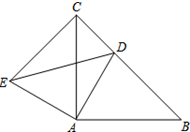 已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.
已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.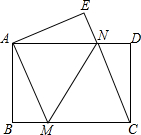 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N. 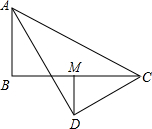 在Rt△ABC中,∠B=90°,AD平分∠BAC,CD⊥AD,垂足为D,DM⊥BC.
在Rt△ABC中,∠B=90°,AD平分∠BAC,CD⊥AD,垂足为D,DM⊥BC.