题目内容
已知4x+y=1,-1<x≤2,求y的取值范围.
考点:一次函数的性质
专题:计算题
分析:先变形得到一次函数y=-4x+1,再分别计算出自变量为-1和2时的函数值,然后根据一次函数的性质确定y的取值范围.
解答:解:∵4x+y=1,
∴y=-4x+1,
当x=-1时,y=4+1=5;当x=2时,y=-8+1=-7,
∴当-1<x≤2,y的取值范围为-7≤x<5.
∴y=-4x+1,
当x=-1时,y=4+1=5;当x=2时,y=-8+1=-7,
∴当-1<x≤2,y的取值范围为-7≤x<5.
点评:本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.

练习册系列答案
相关题目
A、B两城相距720km,普快列车从A城出发120km后,特快列车从B城开往A城,6h后两车相遇.若普快列车是特快列车速度的
,且设普快列车速度为xkm/h,则下列所列方程错误的是( )
| 2 |
| 3 |
A、720-6x=6×
| ||
B、720+120=6(x+
| ||
C、6x+6×
| ||
D、6(x+
|
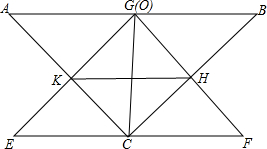 如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H.
如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H. 如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,其中能使△ABC≌△AED的条件有
如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,其中能使△ABC≌△AED的条件有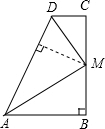 如图,AB⊥BC,CD⊥BC,M是BC上的一点,连接DM、AM,且AM、DM分别平分∠DAB和∠ADC,试判断BM和CM的大小关系,并说明理由.
如图,AB⊥BC,CD⊥BC,M是BC上的一点,连接DM、AM,且AM、DM分别平分∠DAB和∠ADC,试判断BM和CM的大小关系,并说明理由.